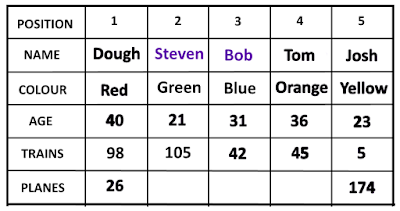
The Spotting Contest
During a recent plane and train spotting contest, five eager entrants
were lined up ready to be tested on their spotting ability.
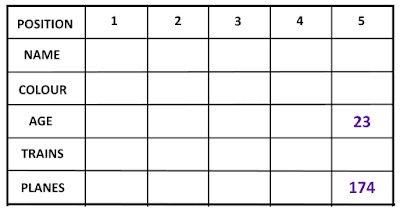
They had each spotted a number of planes (26, 86, 123, 174, 250) and a number of trains (5, 42, 45, 98, 105). From the clues below, can you determine what colour shirt each was wearing, their position, their age (21, 23, 31, 36, 40) and the number of trains and planes spotted?
They had each spotted a number of planes (26, 86, 123, 174, 250) and a number of trains (5, 42, 45, 98, 105). From the clues below, can you determine what colour shirt each was wearing, their position, their age (21, 23, 31, 36, 40) and the number of trains and planes spotted?
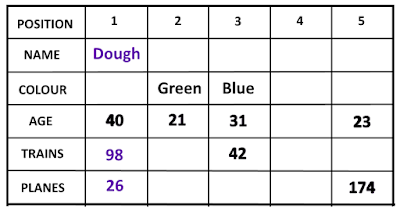
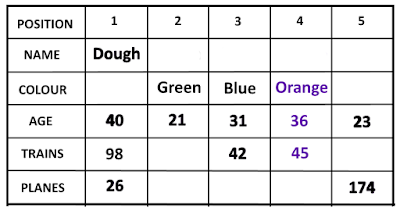
1. Bob spotted 44 less trains than planes.
2. Tom was 36 years old.
3. The person on the far right was 8 years younger than Bob, and spotted 174 planes.
4. Josh was wearing a yellow shirt and spotted 37 trains fewer than Bob.
5. The person who was wearing a green shirt, was 19 years younger than the person to his left.
6. Steven spotted 105 trains and 250 planes.
7. The person in the center was 31 years old, was wearing a blue shirt and spotted 42 trains.
8. Doug, who was on the far left, spotted 26 planes, and spotted 72 trains more than planes.
9. The person who was wearing a red shirt was 4 years older than Tom and was not next to the person wearing a blue shirt.
10.The person who was next to the 31 year old, but not next to the person who spotted 26 planes, was wearing a orange shirt, and spotted 45 trains.
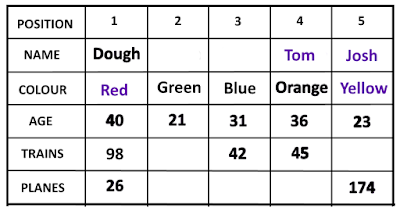
Here are final STATS of the contest!