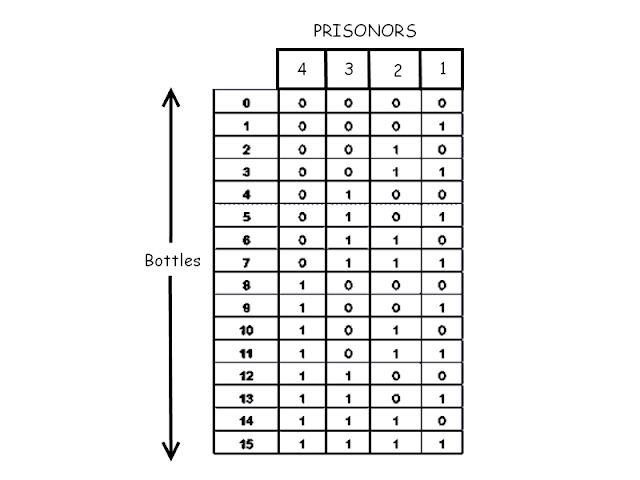
100m Running Race

Lavesh, Bolt, and Lewis race each other in a 100 meters race. All of them run at a constant speed throughout the race.

Lavesh beats Bolt by 20 meters.
Bolt beats Lewis by 20 meters.

How many meters does Lavesh beat Lewis by ? 

Know here the answer! 

Source 

Winner Beats Second Runner Up by...

What was the question? 

Let Lavesh's speed be 10 m/s. Then he must have taken 10 seconds to finish the race. Since Bolt was beaten by Lavesh by 20 m he must have run 80m when Lavesh finished race in 10 seconds (t=10). So his speed would be 8 m/s.

Now Bolt requires 100/0.8 = 12.5 seconds to finish the race. When he finished, Lewis was 20m behind i.e. 80m from starting point at t = 12.5. So Lewis speed is 80/12.5 = 6.4 m/s

At t = 10 seconds, when Lavesh finished his race Lewis must be at 6.4 x 10 = 64 m from starting point. Hence Lavesh beats Lewis by 100 - 64 = 36 m.

Another method.

Let L be the speed of Lavesh, B be the speed of Bolt & W be that of Lewis. Then,

L/B = 100/80 = 5/4

L = (5/4) B  .......(1)

Similarly,

B/W = 100/80 = 5/4

B = (5/4) W .......(2)

Putting (2) into (1),

L = (5/4) x (5/4) W

L/W = 25/16

L = (25/16) W

For given time t, when Lavesh finished the race,

Distance by L/ Distance by W = 25 / 16

100 m/ Distance by W = 25 / 16

Distance by W = (16 x 100) / 25 = 64.

  
So when Lavesh finished cross line at 100 m, Lewis was at 64m i.e. 36m behind. In other words, Lavesh beats Lewis by 100 - 64 = 36 m.

Test Of Poison

You are the ruler of a medieval empire and you are about to have a celebration tomorrow. The celebration is the most important party you have ever hosted. You've got 1000 bottles of wine you were planning to open for the celebration, but you find out that one of them is poisoned.

The poison exhibits no symptoms until death. Death occurs within ten to twenty hours after consuming even the minutest amount of poison.

You have over a thousand slaves at your disposal and just under 24 hours to determine which single bottle is poisoned.

You have a handful of prisoners about to be executed, and it would mar your celebration to have anyone else killed.

What is the smallest number of prisoners you must have to drink from the bottles to be absolutely sure to find the poisoned bottle within 24 hours? 

Here is the test designed for it! 

Source 

Test To Detect The Poison

Here is the challenge for us! 

Here binary number system can come to rescue. Just for a  moment, let's assume there are 15 bottles. Now let's number the bottles from 1 to 15. To test these 15 bottles we need 4 prisoners as below. Let's number the prisoners from in descending 4 to 1.

Wherever 1 is written for the particular bottle number, that bottle should be given to particular prisoner. Otherwise should not.

So for the specific bottle with unique number a specific combination of prisoners (they are bits here) would be formed. 

For example, if bottle labeled as 11 has a poison then prisoner no. 4,2,1 would die. In other words, if prisoner 4 & 2 die then the bottle no. 10 had poison.

For 16th bottle we would have needed 1 more prisoner.

In similar way, to test 1000 bottles, we need 10 prisoners (2^10=1024). Depending on what combination of prisoner die we can determine which bottle had poison. If prisoners numbered from 10 to 1 & if prisoner 10,8,6,3 & 2 die then bottle no.678 (binary - 1010100110) must had poison. Since the poison takes some time to take effect, even if prisoners taste this bottle, we still would have time to test rest of all bottles in given binary pattern. 

  Poisonous Bottle

In case there were 1025 bottle, we would have needed 11 prisoners.

 

How Many Apples in a Basket?

In a guess game , five friends had to guess the exact numbers of apples in a covered basket.Friends guessed as 22 , 24, 29 , 33 , 38, but none of guess was right.The guesses were off by 1, 8, 6, 3, and 8 (in a random order).

From this information, can you determine the number of apples in a basket ?

Logic to get the answer! Click here! 

Source 

Number of Apples in a Basket

What was the game? 

There are 2 guesses which were off by 8. That means exact number must be guess (1) + 8 & guess (2) - 8. So those 2 guess must differ by 16 from each other. And there are 2 guesses in given list differing by 16 & those are 22 & 38. Hence the exact number of apples in a covered basket is 30. Let's verify with all guess & errors.

22 + 8 = 30

24 + 6 = 30

29 + 1 = 30

33 - 3 = 30

38 - 8 = 30

Clues From Talk About Boats

At the local model boat club, four friends were talking about their boats. There were a total of eight boats, two in each color, red, green, blue and yellow. 

1. Each friend owned two boats. 

2. No friend had two boats of the same color.

3. Alan didn't have a yellow boat.

4. Brian didn't have a red boat, but did have a green one.

5. One of the friends had a yellow boat and a blue boat and another friend had a green boat and a blue boat. 

6. Charles had a yellow boat. 

7. Darren had a blue boat, but didn't have a green one.

Can you work out which friend had which colored boats? 

Know here step by step process of finding owners! 

Source 

Owners Of Boats

What's the task given? 

First let's rewrite all the clues here.

1. Each friend owned two boats. 

2. No friend had two boats of the same color.

3. Alan didn't have a yellow boat.

4. Brian didn't have a red boat, but did have a green one.

5. One of the friends had a yellow boat and a blue boat and another friend had a green boat and a blue boat. 

6. Charles had a yellow boat. 

7. Darren had a blue boat, but didn't have a green one.

Let's make 2 set of 4 colors of boats. Below is the table with owners in row & color of boats in columns.  

Below are clues which giving clear idea of owner of particular colored boat.

3. Alan didn't have a yellow boat.

4. Brian didn't have a red boat, but did have a green one.

6. Charles had a yellow boat.

7. Darren had a blue boat, but didn't have a green one.

We will fill this table one by one as per clues given.

Now, consider the first part of this clue.

5. One of the friends had a yellow boat and a blue boat.

Now Alan won't have this combination as he doesn't own yellow boat at all. The Brian already had green boat, so he too can't have this combination as in that case he would own 3 boats.

Let's assume Charles had this combination then other would have boats as below.

Corrupt Courier Service - Puzzle

Two friends Sachin & Rahul are living in two different towns. Sachin wanted to send few diamonds to Rahul but there is big problem. Both Sachin & Rahul have lot's of boxes which can be locked with locks & keys. Both have multiple locks. There is only 1 courier service which can ship those diamonds & there is no other way. Even worse is that workers at that courier service have bad habit of stealing the goods from packages. But one good thing is that they don't take efforts to break locks if boxes being shipped are locked. 

How Sachin should send diamonds to Rahul?

This is what Sachin should do? 

Dealing With Corrupt Courier Service

What was the situation? 

What should Sachin do is that send diamonds in box locked with his own lock & key. On receiving that box, Rahul should put his own lock on the box without disturbing lock placed by Sachin. With 2 locks, he should send that box again to Sachin. Now, Sachin should remove his lock with his key & keep lock placed by Rahul intact. Finally, he need to send back the box with Rahul's lock on it.

Now Rahul can unlock the box using key that he has to get diamonds.

In this way, in every journey there would be always lock (or 2 locks in journey of box from Rahul to Sachin) on the box. So workers won't get any chance to steal those diamonds.   

Optimize Weighing Balance

You can place weights on both side of weighing balance and you need to measure all weights between 1 and 1000. For example if you have weights 1 and 3,now you can measure 1,3 and 4 like earlier case, and also you can measure 2,by placing 3 on one side and 1 on the side which contain the substance to be weighed.

So question again is how many minimum weights and of what denominations you need to measure all weights from 1kg to 1000kg. 

We require only......Click here to know! 

Source 

Optimisation Of Weighing Balance

What was the task given? 

Just for a moment, let's assume we have to weigh 1 to 30 Kg. Now you can weigh all those with

1,          2,          4,         6,          8,         10..........30

1           2, (2+1), 4, (4+1),6, (6+1), 8,(9+1),10..(29+1),30   .......For middle weights.


Now 6 can be weighed as 2 + 4 & 10 can be weighed as 2 + 8. We can eliminate those. That means we require only

1,        2,         4,          8,         16,

So we need weights of powers of 2.

Now if subtraction is allowed then,we require

1,        3,         6,          9,          12,          15,         18,...............30

For all weights ,

1, (3-1),3, (3+1), (6-1), 6, (6+1), (9-1),9,         12,         15,............30   

But 6 can be weighed as 9-3 , 12 as 9+3, 15 as 27-(9+3). So we can eliminate 6,12,15... This leaves only

1,         3,        9,        27,

In short, we need power of 3 only.      

For the given problem we need to weight 1 to 1000 Kg with subtraction allowed. So the maximum power of 3 that is less than 1000 is 7. To conclude, we require only 7 weights as below.

1,3,9,27,81,243,729 

Game Of Death - Josephus Problem

There are 100 people standing in a circle in an order 1 to 100. No. 1 has a sword. He kills the next person (i.e. No. 2) and gives the sword to the next (i.e. No. 3). All people do the same until only 1 survives. Which number survives at the last?

Find who survived? 

Source 
 

The Man Surviving in Game Of Death

What was the problem? 

First let's make it very simple by who are surviving after each round.

Round 1 : 1,3,5,7,9,11,13,15..........87,89,91,93,97,99

Round 2 : 1,5,9,13,17.........89,93,97 

Round 3 : 1,9,17,25,33,41,49,57,65,73,81,89,97

Round 4 : 9,25,41,57,73,89

Round 5 : 9,41,73

Round 6 : 9, 73

At round 5, 9 kills 41 & passes sword to 73. So 73 kills 9 & survives.

Round 7 : 73

Now let's analyze  how this happens & trick to get answer at the quickest.

Just for a moment let's assume there were 16 standing in circle.

Now after each round survived people are,

Round 1 : 1,3,5,7,9,11,13,15

Round 2 : 1,5,9,13

Round 3 : 1,9

Round 4 : 1

After round 2, when 9 kills 13 & passes sword to 1.

And in round 4, 1 kills 9. So 1 forms pair with other in every round.

Now imagine there were 17 people in circle. 

Erroneous Statement

Read the statement below. The task is given within the statement itself.

They are three errirs in this question. Can you find them ? 

Hint: While first 2 errors can be easily spotted for the third one you need to think little more. Pay attention what statement is suggesting.


Errors listed here!

 

Errors In The Statement

But what was the statement? 

Here is 'that' statement once again.

They are three errirs in this question. Can you find them ?

1. They ......Should be There.

2. errirs......Must be spelled as errors.

3. The statement states 3 but there are only 2 errors. 

Finding Horses For Courses

There are 25 horses among which you need to find out the fastest 3 horses. You can conduct race among at most 5 to find out their relative speed. At no point you can find out the actual speed of the horse in a race. Find out how many races are required to get the top 3 horses. 

Click here for logical answer! 

Source 

Races To Find Horses For Courses

What was the task? 

First we need to make 5 groups of 5 horses each. Let's put each group on race & note down rank of each horse & corresponding group. This requires 5 races.

Taking out winner of each group aside. In a next race, winner of each group run & fastest winner is found. Total 6 races are conducted till now.

Now let's name group of fastest winner as A, second fastest winner as B & so on as C, D, E. Each horse would be identified by it's group name & rank as Group.Rank. For example, B.3 means the horse that came 3rd in group B & D.5 is horse that came last in group D.

For next race, we can eliminate few. Let's remind we have to find 3 fastest horses. Now let's logically eliminate few horses. Those horse for which we are sure that at least other 3 are faster than those will be eliminated.

1. Now A.1, B.1 & C.1 are faster than D.1 & E.1. So D.1 & E.1 & respective groups eliminated straightaway.

2. The C.2 (& other members of C) eliminated as A.1, B.1, C.1 are faster ones.

3. The B.3 (& other member of B) eliminated as at least A.1, B.1, B.2 are faster ones.

4. Similarly, A.4 & A.5 have 3 horses ahead as A.1, A.2 & A.3.

5. A.1 is already proved it's fastest among all, so no need to re race by taking it.

Tic Tac Toe Challenge

You all must have played Tic Tac Toe in your childhood. Lets put your skills to test. Can you place six X (crosses) in a Tic Tac Toe board without making three in a row in any way?

How? View here! 

Tic Tac Toe Skills Tested

What was the challenge? 

It's pretty simple. All you need to do is not to start from the center!

Another way,

Grandma's Birthday And Troll Toll

You are on your way to visit your Grandma, who lives at the end of the valley. It's her birthday, and you want to give her the cakes you've made.

Between your house and her house, you have to cross 7 bridges, and as it goes in the land of make believe, there is a troll under every bridge! Each troll, quite rightly, insists that you pay a troll toll. Before you can cross their bridge, you have to give them half of the cakes you are carrying, but as they are kind trolls, they each give you back a single cake.

How many cakes do you have to leave home with to make sure that you arrive at Grandma's with exactly 2 cakes?

How many you should carry? Know here!

Source 

Cakes For Grandma's Birthday

What's between you & grandma's birthday celebration? 

No need to overthink on this. Just carry 2 cakes.

At each toll they would take 1 ( half of 2 ) & would give back 1.

So after each toll you would carry 2 cakes & last toll wouldn't be an exception.

Squares From Squares Challenge

In the picture that is attached with this question, you can find a square which comprises of four little squares inside it. Consider this square to be made with matchsticks. You have to remove two matchsticks such that only two squares remain instead of five.How will you do it ?

Make it 2!

Challenge accepted here! 

Source 

Squares From Squares Challenge Accepted

What was the challenge? 

All that you need to do is that remove these 2 match sticks labelled in figure below.

So we get exactly 2 squares as below.

What is Sister-7 doing ?

There are seven sister in a house in a village where there is no electricity or 

any gadget.

Sister-1: Reading Novel

Sister-2: Cooking

Sister-3: Playing Chess

Sister-4: Playing Sudoku

Sister-5: Washing clothes

Sister-6: Gardening


what is Sister-7 doing ? 

She must be..... 

Source 
 

Playing The Chess Alone?

First read the question. 

Sister -7 must be playing Chess with Sister-3.Remember there is no gadget in room.So sister -3 must not be playing Chess on a smartphone, tablet, laptop or desktop PC (no electricity). Every other activity can be done individually but for playing Chess you need partner at the other end.

A Clever Trader At Checkpoints

Anabelle is a clever trader of rare artifacts. Each day she carries three boxes with each filled with thirty artifacts. The boxes can't hold more than that. She travels far of northern lands to sell these artifacts but on way, she comes across thirty checkpoints where she has to shed one of the artifact for each sack to the authorities for letting her pass.

How many artifacts will be left with her when she reaches her destination crossing all the check points ?  

How she managed to save some? Find here! 

Source
 

A Cleaver Trader's Deal At Checkpoints

What was the situation?

Without any work to brain if she travels as it is through all checkpoints then at the end nothing would be left with her. Because at each checkpoint she has to shed 3 artifacts so at 30 checkpoints she has to shed 3 x 30 = 90 artifacts if she gives artifact from each box. And she has only 90 artifacts.

As a clever trader, she starts shedding artifacts from one box at each checkpoint. At first 10 checkpoints, 1 box would be emptied & 30 artifacts paid at checkpoints.

For next 15 checkpoints, she sheds all artifacts from second box thereby paying 30 artifacts.

For final 5 checkpoints, now she has to shed only 5 artifacts from third box with 25 artifacts remaining in the box.

So 25 artifacts will be left with her when she reaches her destination crossing all the check points.

Initial Amount in Wallet?

On the festival of Raksha Bandhan (holy festival where brother-sister relationship celebrated), Mayank decides to visit his 3 sisters. He takes certain amount with in his wallet & goes to first sister. While without his notice first sister puts equal amount of money as in wallet. After tying rakhi, Mayank gifts her Rs.2000. Now he moves to second sister. While Mayank takes a breakfast, the second sister secretely doubles the money that was in Mayank's wallet. Again after tying rakhi, Mayank gifts her Rs.2000. At third sister's home, while he enjoys delicious lunch cooked by his sister, third sister doubles money in his pocket. Once again after tying rakhi, Mayank gifts third sister Rs.2000.Now there were Rs.5000 in his wallet.

How much amount Mayank had taken while leaving his home?

How much amount? Find it here! 

Simple Calculation for Initial Amount

What was the puzzle? 

We need to go backward to get the answer.

3. At third sister's home he had 2000 + 5000 = 7000. So before visit he had 7000 / 2 = 3500.

2. At second sister's home he had 3500 + 2000 = 5500. This 5500 were doubled from his existing 2750 by her second sister.

1. At first sister's home he had 2750 + 2000 = 4750. His first sister had added 4750 / 2 = 2375 to his wallet in which there were Rs. 2375 already.

So Mayank took Rs. 2375 with him in his wallet while he left home.

However, Mayank must had idea of that his sisters added money to his wallet without his attention.

 

Abnormal Looking Normal Puzzle

A donkey travels the exact same distance daily. Strangely 2 of his legs

travels 40 kilometers and the remaining two travels 41 kilometers. 

Obviously 2 donkey legs cannot be a 1km ahead of the other 2.

The donkey is perfectly normal. So how come this be true ?

 I'm perfectly normal!

Why so? Find it here! 

Source 

That Looks Perfectly Normal

What was looking abnormal? 

The donkey is moving on a circular path. Hence, his 2 legs on right (or left depending on moving clockwise or anticlockwise) moves along a circle having lesser radius than circle on which left legs are moving. The difference in circumferences of circles accounts the difference in distance traveled.

Winner Deserving The Scholarship

This is my favorite puzzle which I had read in a newspaper. It really makes you to think more & more logically to get the answer. I had posted it back in July but re posting it here.

"The scholarship will be awarded," said the head to three candidates - Chuckles, Wombat & Breeze - "to the winner in this little competition. I am going to chalk a cross, which will be either a green or a red cross. I shall then ask each one who can see a green cross to hold his hand up; and take his hand down as soon as he can tell me what his own cross is. He must, of course, be able to explain how his answer is arrived at. Kindly close your eyes for 10 seconds."

He chalked a green cross on all three foreheads. "Go!"

All three hands shot up in air ; that of Chuckles was almost immediately lowered. "My cross is green , Sir"

How did Chuckle know?
  
Read here how the story unfolds!



 

Popular Missing Square Puzzle

How many number of times you have come across this image?

By now, you might have accepted the solution.

"The hypotenuse is bulged in bottom figure which accounts area equal to missing square!"

But is this really a solution to this puzzle? The issue illustrated in clear manner here!

And my opinion is here!

And how creator did manage to create that 'missing' square is illustrated here!

 

Jumping Safely From 33rd Floor?

A man was gazing through the window of the 33rd floor of the building. He suddenly opened the window and jumped on the other side of the window. On landing the floor, there was not a sheer mark of injury on him.

How can that be possible if he did not use any kind of parachute and did not land on a soft surface ? 

  
Why he landed safely? Find Here! 

Jump Causing No Injury

But why to jump? 

The man was cleaning the window of 33rd floor & jumped inside the room through the window after finishing his work. Jumping from few feet from landing floor rarely causes any injury.

Crossing The River In Minimum Time

Four people need to cross a dark river at night. They have only one torch and the river is too risky to cross without the torch. If all people cross simultaneously then torch light won't be sufficient. Speed of each person of crossing the river is different. Cross time for each person is 1 min, 2 mins, 7 mins and 10 mins. 

However 2 can cross together but there is one limitation.If two are crossing the river then it takes time equal to slowest person would take alone. For example, if persons with cross times 1 min & 10 mins are crossing then it would take 10 mins for both to cross the river.

What is the shortest time needed for all four of them to cross the river ? 

  
Find here the efficient way! 

Source 

Efficient Way To Cross The River

What's the challenge? 

Let's name each person by their crossing times as 1,2,7,10.

The instant solution that everyone can think of is using 1 as a usher to guide all. That means 10 & 1 goes, 1 comes back; 7 & 1 goes again 1 comes back and 2& 1 goes finally. This would take 10 + 1 + 7 + 1 + 2 = 21 mins to cross rivers.

Is it really efficient solution? What if we find a way to cross both 10 & 7 in one go & other 1 waiting across to bring back torch.

1. The 1 & 2 goes across but 1 comes back - 2 + 1 = 3 mins required.

2. Now 10 & 7 goes across & send 2 back with torch - 10 + 2 = 12 mins required.

3. Finally after coming back 2 & take 1 across the river - 2 minutes required.

So total 3 + 12 + 2 = 17 minutes required to cross the river for those 4 persons. In first step, 2 can also come back & send 10 & 7. In that case, in second step, 1 has to come back to take 2 across the river. Isn't this a more practical solution? 

Hijacker's Strange Demand!

A man hijacks an aeroplane transporting both passengers (8 of them) and valuable cargo.After taking the cargo, the man demands nine parachutes, puts one of them on, and jumps, leaving the other eight behind. Why did he want other eight?

          I want 9!

Find the reason here! 

Source 

Hijacker's Safe Game!

And how did he play it? 

Had he demanded single parachute how can he be sure that it's not adefective one. He demanded nine with thought that cops would think that he wants to jump with all 9 passengers safely. So cops would not take risk of sending any defective parachute.