The Number Game!

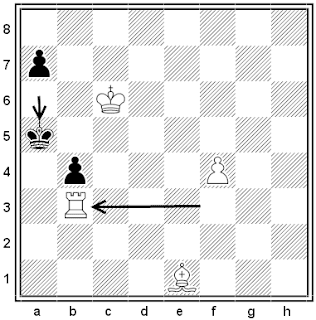
Let’s play a game. You name an integer from 1 to 10. Then we’ll take turns adding an integer from 1 to 10 to the number our opponent has just named, giving the resulting sum as our answer. Whoever reaches 100 first is the winner.

You go first. What number should you choose?

This is how you can be winner!

Winning The Number Game!

What was the game?

Here the player whose number 'forces' sum to fall in range of 90-99 will be ending on losing side. 

That means, somehow if you 'force' the total at some point to 89 then opponent has to fall in the range of 90-99 with his number. 

To get 'door' to total 89 you have to force the previous sum to 78 so that opponent is forced to open a 'door' for total 89 for you.

And so on backward you have to make stops at 67, 56, 45, 34, 23, 12, 1.

So you have to start with 1 & achieve all above milestones.

Let's verify our conclusion. Suppose you started with 1.

You       Sum      Opponent    Sum

1            -             8              9
3           12            5              17
6           23            7              30
4           34            9              43
2           45            4              49
7           56            10            66
1           67            3              70
8           78            2              80
9           89            4              93
7           100           

YOU WIN!

CheckMate The Opponent in 2 Moves!

Can White checkmate Black in two moves from this position?

Here are those 2 moves! 

2 Moves to CheckMate the Opponent

Where the game stands?


1.Move Rook to b3 i.e. perform Rb3.

2.That will force opponent to move king to a5 i.e. execute Ka5.

3. Finally,now move Rook to a3 (Ra3) and Checkmate the opponent.

Case of 3 Identical Notebooks

Three people all set down their identical notebooks on a table. On the way out, they each randomly pick up one of the notebooks. What is the probability that none of the three people pick up the notebook that they started with?

That's correct probability!

Probability in Case of 3 Identical Notebooks

What was the case?

Let's name peoples as Person - 1, Person - 2, Person - 3 and their notebooks as Notebook - 1, Notebook - 2 and Notebook 3 respectively.

Now there can be 6 ways 3 notebooks can be distributed among 3 persons like below.

(Here, for convenience, 3 different colors are assigned to the notebooks of 3 persons.)

As we can see, there are only 2 cases, where the each of person not getting own notebook. In rest of cases, at least 1 person got own notebook & notebooks of others are shuffled between 2.

So the probability that none of the three people pick up the notebook that they started with is 2/6 = 1/3. 

Unfair Game of Strange dice

Katherine and Zyan are playing a game using strange dice. Each die is a cube with six sides. Katherine's die has sides numbered 3, 3, 3, 3, 3, and 6. Zyan's die has sides numbered 2, 2, 2, 5, 5, and 5.

To play the game, Katherine and Zyan roll their dice at the same time and whoever rolls the higher value wins. If they play many times, who will win more frequently, Katherine or Zyan?

This person will be winning more! 
 

Advantage in Unfair Game of Strange Dice

What was the game?

Shortest Way : 

Katherine's die has sides numbered 3, 3, 3, 3, 3, and 6. And Zyan's die has sides numbered 2, 2, 2, 5, 5, and 5. That means whenever Zyan rolls a 2 then Katherine will always win. The probability that Zyan rolls 2 is 3/6 = 1/2. So in half of the cases, the Katherine will be winner of the game. Moreover, whenever, Zyan rolls a 5, Katherine can win if she rolls a 6. In short, in more than half cases, Katherine will win hence she has more advantage in this game.


Precise Way : 

Katherine will win if

1. Zyan rolls a 2 with probability 3/6 = 1/2

2. Zyan rolls a 5 (probability 3/6 = 1/2) and Katherine rolls a 6 (probability 1/6). So the probability for this win = 1/12.

Hence, Katherine has got 1/2 + 1/12 = 7/12 chances of winning.

Zyan will win if he rolls a 5 (probability 1/2) and Katherine rolls a 3 (probability 5/6) with probability = 1/2 x 5/6 = 5/12.  

That proves, Katherine has more chances (7/12 vs 5/12) of winning this game. 

Another Way : 

There can be 36 possible cases of numbers of cubes out of which in 15 cases Zyan seems to be winning and in 21 cases, Katherine is winning. Again, Katherine having more chances of winning (21/36 = 7/12) than Zyan (15/36 = 5/12). 

Search Number for '?'

Can you find the number for the '?' ?

Skip to the answer! 

In The Search of Number for '?'

Here is the question! 

First two equations clearly indicates it must be straightforward a + b equation.

Now if you observe closely all the equations, then you can find that the number never exceeds 8. So there are chances that all these number are in octal number system i.e. base 8 numbers.

Hence 11 in third equation is actually 8 in decimal. That's why 7 + 8 = 15 where decimal 15 is converted to octal 17. 

Verifying third equation as 15 + 16 = 31 in decimal is actually 17 + 20 = 37.

On the similar note, we have fourth equation in decimal as 31 + 32 = 63 which can be converted to octal as 37 + 40 = 77.

Hence the search for number in place of '?' ends with the number 77.

Profit Or Loss Or No-Profit No-Loss?

A man buys a horse for $60. He sells the horse for $70. He then buys the horse back for $80. And he sells the horse again for $90. How much profit did he make or did he loose in transaction? Or did he break even?

Confused? Find the right answer here!

And He Earned A Profit!

But what was the deal?

The confusion starts when he he buys same horse again. But if we look at it as two different transactions then it pretty straightforward.

At first he buys horse for $60 & sells it for $70. Here, he makes profit of $10. This is one transaction.

In next transaction, he buys same horse for $80 & sell the same for $90. Again, here he makes profit of $10.

In this way, the total profit he earns from these transactions is of $20.  

Difficult Puzzle of Sum and Product

Sum Sam and Product Pete are in class when their teacher gives Sam the Sum of two numbers and Pete the product of the same two numbers (these numbers are greater than or equal to 2). They must figure out the two numbers.

Sam: I don’t know what the numbers are Pete.

Pete: I knew you didn’t know the numbers… But neither do I.

Sam: In that case, I do know the numbers.

What are the numbers?

Want to know those numbers?

Solution - Difficult Puzzle of Sum and Product

Wait, read the puzzle once! 

Let's remind that the numbers are greater than or equal to 2; means those can't be either 0 or 1.

Now take a look at what Sam & Pete says - 

Sam: I don’t know what the numbers are Pete.

Pete: I knew you didn’t know the numbers… But neither do I.

Sam: In that case, I do know the numbers.

If Sam was told 4 then straightway he would have numbers 2,2 in mind as 3,1 combination is invalid.

If teacher had told Sam 5 as a sum then too Sam had correct pair of numbers 2,3 immediately as 4,1 or 5,0 are invalid combinations. 

So Sam must have at least number 6. Valid combinations for this sum are (2,4), (3,3).

If it was (3,3) then Pete would had 9 & he would have identified this combination correctly as (9,1) is not valid combination. Since he too didn't know exact numbers, it must be some different combination.

And if teacher had told Pete 8 then too he would have easily figured out correct combination of (2,4) as (8,1) is not valid.

So Pete can't have number 1,2,3,4,5,6,7, 8 or 9 or 11.

Now if he had 10 then only possible combination (2,5) and he would have that immediately. So he wouldn't have made the statement that he too didn't know numbers.

Let's assume that he had number 12 as product. Now in this case valid combinations are (2,6), (3,4).  The sums of these valid combinations are 8 & 7 respectively.

Now depending on what sum the Sam had; he can identify the correct pair of numbers easily.

Even/Even x Even - Odd ?

Can an even number, divided by another even number, times another even number ever equal an odd number?

The three even numbers can be different numbers.



Did you too think same? 

Even/Even X Even = Odd!

What was the question?

Absolutely, it's possible! Take a look at the examples below.

Totally depends on the what result of Even/Even comes out & what is the Even number that is being multiplied with the result.

What color was the bear?

I left my campsite and hiked south for 3 miles. Then I turned east and hiked for 3 miles. I then turned north and hiked for 3 miles, at which time I came upon a bear inside my tent eating my food! What color was the bear?

Yes, it can be answered!

'THIS' Was The Color of Bear!

Wait,first read the question! 

There is only one place on earth where when you hike 3 miles south then 3 miles east followed by 3 miles north & eventually end at the same starting point. And that place is north pole. 

Only Polar bears can survive on north pole; and they are white in color.

Hence, the bear found must be of white color. 

Count The Number of Kids

Fourteen of the kids in the class are girls. Eight of the kids wear blue shirts. Two of the kids are neither girls or wear a blue shirt. If five of the kids are girls who wear blue shirts, how many kids are in the class?

Find The Count Here!
 

Count of Number of Kids.

 Read the problem first!

 Let's recollect all the data given in the question.

1.Fourteen of the kids in the class are girls.

2. Eight of the kids wear blue shirts. 

3.Two of the kids are neither girls or wear a blue shirt.

4.Five of the kids are girls who wear blue shirts.

Now, (3) clearly suggests that there are 2 boys who are not wearing blue shirts. 

From (5) and (2), it's clear that 3 of 8 kids who are wearing blue shirts are boys as 5 of them are girls.

Above 2 conclusions indicates that there are total 5 boys in the class; 2 not wearing blue shirts and 3 wearing blue shirts.

But as per (1), there are 14 girls in a class. 

Hence, total 14 + 5 = 19 kids are there in a class.

Three Hat Colors Puzzle

A team of three people decide on a strategy for playing the following game.  

Each player walks into a room.  On the way in, a fair coin is tossed for each player, deciding that player’s hat color, either red or blue.  Each player can see the hat colors of the other two players, but cannot see her own hat color.  

After inspecting each other’s hat colors, each player decides on a response, one of: “I have a red hat”, “I had a blue hat”, or “I pass”.  The responses are recorded, but the responses are not shared until every player has recorded her response.  

The team wins if at least one player responds with a color and every color response correctly describes the hat color of the player making the response.  In other words, the team loses if either everyone responds with “I pass” or someone responds with a color that is different from her hat color.

What strategy should one use to maximize the team’s expected chance of winning?

These could be the strategies to maximize the chances of winning!

Three Colors Hats Puzzle - Solution

What's the puzzle? 

There can be two strategies to maximize the chances of winning in the game.

STRATEGY - 1 :   

There are 8 different possible combinations of three color hats on the heads of 3 people. If we assume red is represented by 0 & blue by 1 then those 8 combinations are - 

Here only 2 combinations are there where all are wearing either red or blue hats. That is 2/8 = 25% combinations where all are wearing hat of same color and 6/8 = 75% combinations where either 1 is wearing the different colored hat than the other 2.  In short, at least 2 will be wearing either red or blue in 75% of combinations.

Now for any possible combination, there will be 2 hats of the same color (either blue or red). The one who sees the same color of hats on heads of other two should tell the opposite color as there are 75% such combinations. That will certainly increase the chances of winning to 75%.

STRATEGY 2 :    

Interestingly, here 3 responses from each member of team are possible viz RED (R), BLUE (B) and PASS (P). And every member can see 3 possible combinations of hats on the heads of other 2 which are as 2 RED (2R),  2 BLUE (2B) and 1RED:1BLUE (RB). See below.

Let's think as instructor of this team. We need to cover up all the possible 8 combinations in form of responses in the above table. 

For every possible combination, at least 1 response need to be correct to ensure win. But out of 9 above, 3 responses of 'PASS' are eliminated as they won't be counted as correct responses. So we are left with only 6. Let's see how we can do it.

First of let's take case of 2R. There are 2 responses where A sees 2 RED hats (000,100). We can't make sure A's response correct in both cases. So let A's response for this case be R. So whenever this 000 combination will appear A's response will secure win.

After covering up 000, let's cover up 001. For that, C's response should be B whenever she sees 2 red hats on other 2. And only left response P would be assigned to B.

So far,we have covered up these 2 combination via above responses.  

--------------------------------------------------------------------------

Now, let's take a case of 2B. A can see 2B hats whenever there 011 or 111 appears. Since A's R response is already used previously, let B be her response in the case. So the combination 111 will be covered up with A's response.  

B can see 2B hats in case of 101 or 111. Since 111 is already covered above, to cover up 101, B should say R whenever she sees 2 BLUE hats on the heads of other 2. With this only response left for C in case of 2B is P.

 
With these responses, we have covers of so far,

 
 -------------------------------------------------------------------------

After filling remaining 1 possible response in response table for every team member in case of 1 RED and 1 BLUE hat, 

 B's response as BLUE in this case will ensure win whenever 011 or 110 combination will appear. Similarly, C's response as a RED will secure win whenever 010 or 100 appears as a combination.

------------------------------------------------------------------------------

In this way, there will be at least 1 response correct for every possible 8 combinations. This strategy will give us 100% chances of winning this game!

The above table shows who is going to respond correctly for the given combination ( the block of combination & correct response are painted with the same background color).
 
SIMPLE LOGIC : 

The same strategy can be summarized with very simple logic. 

There must be someone to say RED whenever she sees 2 RED hats; someone should say BLUE and remaining one should say PASS. Similarly, one has to say BLUE; other should say RED & third one should say PASS whenever 2 BLUE hats are seen. Same logic to be followed in case of 1 RED and  1 BLUE hats seen. But while doing this, we need to make sure responses are well distributed & not repeated by single member of team (See table below).