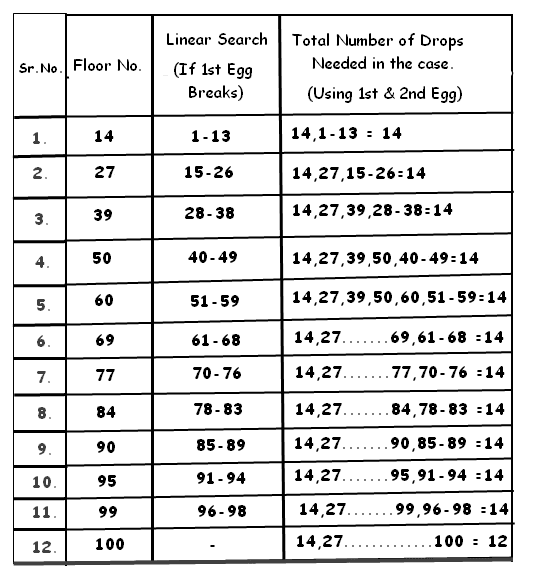
Escape Safely to The Ground!

You find yourself trapped at top an 800 foot tall building. The surrounding land is completely flat, plus there are no other structures nearby. You need to get to the bottom, uninjured, and can only safely fall about 5feet.

You look down the four walls; they are all completely smooth and featureless, except that one of the walls has a small ledge 400feet above the ground. Furthermore, there are two hooks, one on this ledge, and one directly above it on the edge of the roof. The only tools you have are 600feet of rope, and a knife.

 How do you get to the bottom? 

This should be your strategy! 

Strategy To Land Safely On The Ground

Why strategy needed to be planned?

1.Tie one end of the rope to the to hook and climb down to the ledge.

2. Cut (without dropping) the rope that hangs below the ledge, then climb back to the roof carrying the extra rope that you cut. You now have two lengths of rope: one that is 400 feet long and one that is 200 feet long.

3.At the top, untie the rope from the hook.

 Now setup the ropes like : Tie a small loop at one end of the 200-foot long rope. String the 400-foot long rope through the loop so that half of its length is on either side of the loop. Make sure that the loop is snug enough that the 400-foot long rope won't fall out by itself, but loose enough that you can pull the rope out later.

4. Now, tie the end of the 200-foot rope without the loop to the first hook. The 200-foot long rope lets you climb halfway to the ledge. 

5.For the remaining 200 feet, you carefully climb down the 400-foot rope, which hangs down 200 feet from where it is held by the loop. 

6.Once you get to the ledge, pull the 400-foot rope out of the loop.

7. Finally, tie it to the second hook, and climb the rest of the way to the ground.

Dropping Height For Egg Breakdown!

There is a building of 100 floors.

-If an egg drops from the Nth floor or above it will break.

-If it’s dropped from any floor below, it will not break.

You’re given 2 eggs.

Find N.

How many drops you need to make?

What strategy should you adopt to minimize the number egg drops it takes to find the solution?

'This' should be the strategy! 

Finding The Dropping Height For Egg Breakdown

What was the task?

Let's suppose, the we drop the egg from N the floor & it breaks then we need to do linear search till (N-1) th floor. For example, we dropped egg from 10 the floor & it breaks then we need to test 1-9 floors using 2nd egg to find the exact floor from which the egg breaks on dropping. So the best case would be 10 drops if the first egg breaks when dropped from 10 the floor.But that's only possible if the egg breaks on drop from 10th floor.

The worst case would be when egg doesn't break at 10,20,30,40,50,60,70,80,90 and breaks at 100th floor. Here, once again 91-99 need to be tested using other egg to find exact floor from which egg will break on drop.So in worst case, 19 drops would be needed.

Best way to minimize the number of drops required is to minimize the linear search (91-99 above  in worst case) that we need to do with the second egg after 1st egg breaks on drop from particular floor (100th floor in above worst case).

So after dropping egg from N th floor & if egg doesn't break then instead of going to next Nth floor, better to go N + (N-1) th floor. And now if the egg break here at N + (N-1) th floor then we need to do linear search from (N+1) th floor to N + (N-1) th floor instead of (N+1) th floor to (N + N) th floor. That's 1 less linear search than that needed if we go to the next N th floor if egg doesn't break on drop from Nth floor.

After dropping egg from N + (N-1) th floor, if it doesn't break then we should go the the N + (N-1) + (N-2) th floor.

Adding all instances of drops i.e. drop at Nth, drop at N + (N-1) th , drop at N + (N-1) + (N-2) & so on gives us

N + (N-1) + (N-2) + (N-3).......+1 = N(N+1)/2.

which shouldn't exceed 100 as there are only 100 floors & hence total number of drops must not be greater than 100.

So,

N(N+1)/2 >= 100

N^2 + N - 200 >= 0

This is

This is quadratic equation in form ax^2 + bx + c = 0 where x = [-b +- (b^2 -4ac)^0.5]/2a.

Solving above for N gives,

N = 13.651

Rounding value of N to 14 in the case.

So we should start with floor no. 14 followed by 27,39,50,60,69,77,84,90,95,99,100

In the worst case here total drops needed are only 14. 

For example, if the egg breaks when dropped from 14th floor then for second egg we need to test 1-13 floors to find the exact floor from which egg breaks on the drop. See table below.

Similarly, for example, egg breaks after drop from 50 floor (after testing 14,27,39), we need to test at 51-59 floors by dropping second egg to know the exact floor from where egg breaks on the drop.
 

Murder or Suicide? - What Do You Think?

A dead body lies at the bottom of a multistory building. It looks as though he committed suicide by jumping from one of the floors.

When the detective arrives, he goes to the first floor of the building, opens the closed window, and flips a coin towards the floor. He goes to the second floor and does the exact same thing. He continues to do this until he gets to the top floor of the building.

When he comes back down, he states that it was a murder and not a suicide. How does he know that?

(Entry to the terrace was banned due to some ongoing work).

Read the detective's logic in the case!

Detective's Logic in Murder Mystery

What is the case?

Obviously, the person can't jump with window closed or come outside of the window & close that window from inside.

The detective checks if windows is closed from inside by opening window & flipping the coin toward the floor. He flips the coin to mark the count of that particular floor where window was closed from inside & he has to open it to flip the coin.

At the end, he collects as many coin as floors of that building. So he concludes that no floor had open window from where the person might have jumped.

 
So, he concludes that it was the murder and not the suicide.

Find The Parking Floor

Six people park their car in an underground parking of a store. 

The store has six floors in all. Each one of them goes to different floor.

Simon stays in the lift for the longest.

Sia gets out before Peter but after Tracy.

The first one to get out is Harold.

Debra leaves after Tracy who gets out at the third floor.

Can you find out who leaves the lift at which floor? 

 
Was it really so difficult? 

Finding The Parking Floor

What was the given data? 

The sentence 'The first one to get out is Harold.' suggests that the Harold leaves the lift at the 1st floor.

Similarly, the sentence - 'Simon stays in the lift for the longest.' suggests that Simon leaves he lift at the 6th floor.

Next, sentence - 'Debra leaves after Tracy who gets out at the third floor' suggests Debra leaves the lift at the 3rd floor.

Clearly, the sentence - 'Sia gets out before Peter but after Tracy.' suggests that Sia leaves the lift at the 4th floor.

Also, it is clear that Debra leaves the lift at the 2nd floor and Peter at the 5th floor.

Summary -

Harold leaves at the first floor.

Debra leaves at the second floor.

Tracy leaves at the third floor.

Sia leaves at the fourth floor.

Peter leaves at the fifth floor.

Simon leaves at the sixth floor.