Puzzle : The Fake Coin Challenge!

There are 101 coins out of which 1 is fake, the fake coin is identical to a genuine coin but differs in weight. Using weight balance only twice how can we determine whether the fake coin is heavier or lighter than a genuine coin?

 

 

This is how to do it! 

Fake Vs Genuine Coin Weigh Comparison

This was the challenge!

Remember we are asked to determine whether the fake coin is lighter or heavier when compared with the genuine coin and not to identify the fake coin itself.

Keep aside any one coin. Divide remaining 100 coins into 2 groups of 50 coins each. Put these 2 groups on 2 pans of the balance.

1. If they weigh equal the the coin that is kept aside is fake. Weigh it against any genuine among 100 coins to know whether fake coin is lighter or heavier than genuine.

2. If they are not equal then that means the fake coin either made one side heavier or the other side lighter.

3. Take the heavier group of 50 coins for the next test. Divide them into 2 groups of 25 coins each. 

4. Put 25 - 25 coins on weighing balance. If they weigh equal then that means no fake coin among them which also means the fake coin was in the other group of 50 coins which was lighter in the first weighing. 

Hence, the fake coin is lighter present in the other group of 50 coins making the group slightly lighter compared to group of 50 genuine coins.

4.1. And if the result of weighing 25 - 25 coins is unequal then it's clear that the fake coin is among these 50 coins. Also, it must be heavier making this group to weigh more than the other group of 50 genuine coins in the first weighing.

This way, we can determine whether the fake coin is heavier or lighter than genuine one using the weighing balance only twice.

Sequel : Story of Distribution of Loot

The five pirates mentioned previously are joined by a sixth, then plunder a ship with only one gold coin.

After venting some of their frustration by killing all on board the ship, they now need to divvy up the one coin. They are so angry, they now value in priority order:

1. Their lives
2. Getting money
3. Seeing other pirates die.

How can the captain save his skin?

This is how he should save himself! 

 The Prequel of the story!

Captain's Life Saving Proposal in Sequel

First read the story of sequel!

Let's name all the pirates as Pirate 6,5,4,3,2,1 as per their seniority. Now, the captain should respond with the logic below to save his skin.

Let's consider the cases where there are different number of pirates left on the ship after getting rid of seniors one by one.

----------------------------------------------------------------------------------------------

CASE 1 : 2 Pirates

The captain i.e. Pirate 2 can keep coin with him & obviously vote for himself (1/2 = 50% vote) to approve the proposal.

------------------------------------------------------------------------------------------------

CASE 2: 3 Pirates.

The captain i.e. Pirate 3 offers coin to Pirate 1 to get his support (2/3 = 66%) on proposal. Since, Pirate 1 knows what is going to happen if Pirate 3 dies as crew reduced to 2 Pirates as in CASE 1.

------------------------------------------------------------------------------------------------

CASE 3: 4 Pirates.

The captain i.e. Pirate 4 offers coin to Pirate 2 thereby getting his support (2/4 =50% votes) to get approval on proposal. Again, here Pirate 2 is smart enough to agree on this proposal as he know what will happen if Pirate 4 is eliminated leaving behind 3 pirates on sheep as in CASE 3.

-------------------------------------------------------------------------------------------------

CASE 4: 5 Pirates.
Now the captain i.e. Pirate 5 always will be in danger as he can give only coin to only 1 of remaining 4. So he can 'earn' only 1 vote in support of his proposal i.e. only 2/5 = 40% votes. Hence, there is no way his proposal get approval & he should be ready to die.

-------------------------------------------------------------------------------------------------

CASE 5: 6 Pirates.

Here, Pirate 5 has to agree whatever captain i.e. Pirate 6 offers as if Pirate 6 dies the case reduces to CASE 4 where Pirate 5 can't save himself. However, if both Pirate 6 & Pirate 5 die, then CASE 3 comes into reality where Pirate 2 gets coin. So Pirate 2 would never agree on proposal offered by Pirate 6.

However, if Pirate 6 offers coin to Pirate 4 then he would take it happily as he knows that what will happen of both Pirate 6 & 5 are killed as CASE 3 comes into picture where he has to give coin to Pirate 2 to save himself.

If Pirate 6 offers coin to Pirate 3 as well & earn his support as Pirate 3 also knows what is going to be the case of both 6 & hence 5 get eliminated. The case will be reduced to 4 Pirates as in CASE 3 where Pirate 4 will offer coin to Pirate 2.

The Pirate 6 even choose Pirate 1 to offer coin. Again, Pirate 1 smart to think that what will be the case if 6 & hence 5 are killed. It will be the scenario as in CASE 3 where Pirate 4 offers coin to Pirate 2.

In short, the Pirate 6 will always get support from Pirate 5 always in any case & any one from Pirate 4/3/1 if he offers coin to any one of these three. 

That's how he will get support of 50% (3/6) group to get approval for his proposal thereby saving his own life on approval of proposal offered.

-------------------------------------------------------------------------------------------------

Flipping The Unusual Coins

You have three coins. One always comes up heads, one always comes up tails, and one is just a regular coin (has equal change of heads or tails). If you pick one of the coins randomly and flip it twice and get heads twice, what is the chance of flipping heads again?

Chances of flipping head again are - .......% Click to know!

Chance of Flipping Head Again

What was the problem?

For a coin to always show head on flip we assume both it's sides are heads and the coin which is showing tail always we assume both of it's sides are tails.

There is no way that you have selected tail only coin since there are 2 heads in first 2 flips.

So it could be either head only coin say D coin or regular fair coin say F.

Let H1 and H2 be the sides of head coin and H, T are side of fair coin.

If it's head only coin D, then possible scenarios on 2 flips are -

DH1 DH1
DH1 DH2
DH2 DH1
DH2 DH2

And if it's fair coin F then possible scenarios on 2 flips are -

FH FH
FH FT
FT FH
FT FT

There are total five combinations (all 4 of head coin + first one of fair coin) where there are 2 consecutive heads on 2 flips.

So, the chances that you have picked a head coin is (4/5) and that you picked fair coin is (1/5).

For head coin, the probability of getting head again is 1 and that for fair coin is (1/2).

Since you holding either head coin or fair coin,

Probability (Head on third flip) = 
Probability (You picked Head coin) x Probability (Head on head coin) + Probability (You picked fair coin) x Probability (Head on fair coin) 


Probability (Head on third flip) = (4/5) x 1 + (1/5) x (1/2)

Probability (Head on third flip) = 9/10.

Hence, the chance of flipping head again on third flip is 90%.

Three Hat Colors Puzzle

A team of three people decide on a strategy for playing the following game.  

Each player walks into a room.  On the way in, a fair coin is tossed for each player, deciding that player’s hat color, either red or blue.  Each player can see the hat colors of the other two players, but cannot see her own hat color.  

After inspecting each other’s hat colors, each player decides on a response, one of: “I have a red hat”, “I had a blue hat”, or “I pass”.  The responses are recorded, but the responses are not shared until every player has recorded her response.  

The team wins if at least one player responds with a color and every color response correctly describes the hat color of the player making the response.  In other words, the team loses if either everyone responds with “I pass” or someone responds with a color that is different from her hat color.

What strategy should one use to maximize the team’s expected chance of winning?

These could be the strategies to maximize the chances of winning!

Three Colors Hats Puzzle - Solution

What's the puzzle? 

There can be two strategies to maximize the chances of winning in the game.

STRATEGY - 1 :   

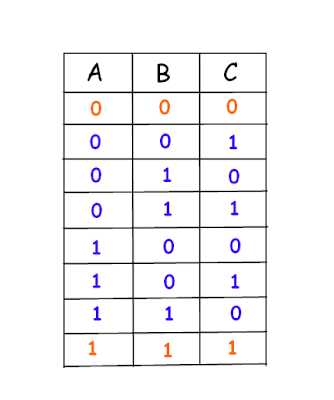
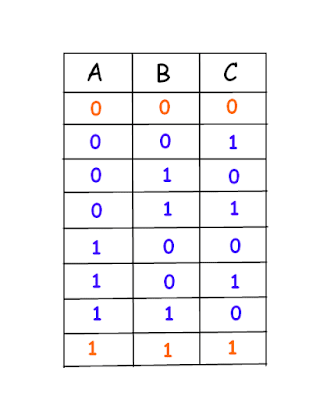
There are 8 different possible combinations of three color hats on the heads of 3 people. If we assume red is represented by 0 & blue by 1 then those 8 combinations are - 

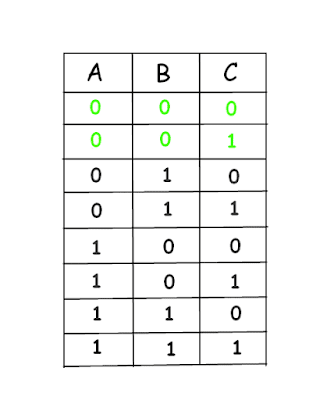
Here only 2 combinations are there where all are wearing either red or blue hats. That is 2/8 = 25% combinations where all are wearing hat of same color and 6/8 = 75% combinations where either 1 is wearing the different colored hat than the other 2.  In short, at least 2 will be wearing either red or blue in 75% of combinations.

Now for any possible combination, there will be 2 hats of the same color (either blue or red). The one who sees the same color of hats on heads of other two should tell the opposite color as there are 75% such combinations. That will certainly increase the chances of winning to 75%.

STRATEGY 2 :    

Interestingly, here 3 responses from each member of team are possible viz RED (R), BLUE (B) and PASS (P). And every member can see 3 possible combinations of hats on the heads of other 2 which are as 2 RED (2R),  2 BLUE (2B) and 1RED:1BLUE (RB). See below.

Let's think as instructor of this team. We need to cover up all the possible 8 combinations in form of responses in the above table. 

For every possible combination, at least 1 response need to be correct to ensure win. But out of 9 above, 3 responses of 'PASS' are eliminated as they won't be counted as correct responses. So we are left with only 6. Let's see how we can do it.

First of let's take case of 2R. There are 2 responses where A sees 2 RED hats (000,100). We can't make sure A's response correct in both cases. So let A's response for this case be R. So whenever this 000 combination will appear A's response will secure win.

After covering up 000, let's cover up 001. For that, C's response should be B whenever she sees 2 red hats on other 2. And only left response P would be assigned to B.

So far,we have covered up these 2 combination via above responses.  

--------------------------------------------------------------------------

Now, let's take a case of 2B. A can see 2B hats whenever there 011 or 111 appears. Since A's R response is already used previously, let B be her response in the case. So the combination 111 will be covered up with A's response.  

B can see 2B hats in case of 101 or 111. Since 111 is already covered above, to cover up 101, B should say R whenever she sees 2 BLUE hats on the heads of other 2. With this only response left for C in case of 2B is P.

 
With these responses, we have covers of so far,

 
 -------------------------------------------------------------------------

After filling remaining 1 possible response in response table for every team member in case of 1 RED and 1 BLUE hat, 

 B's response as BLUE in this case will ensure win whenever 011 or 110 combination will appear. Similarly, C's response as a RED will secure win whenever 010 or 100 appears as a combination.

------------------------------------------------------------------------------

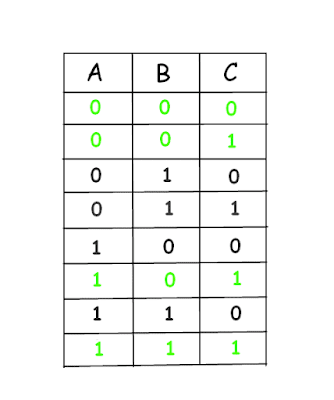
In this way, there will be at least 1 response correct for every possible 8 combinations. This strategy will give us 100% chances of winning this game!

The above table shows who is going to respond correctly for the given combination ( the block of combination & correct response are painted with the same background color).
 
SIMPLE LOGIC : 

The same strategy can be summarized with very simple logic. 

There must be someone to say RED whenever she sees 2 RED hats; someone should say BLUE and remaining one should say PASS. Similarly, one has to say BLUE; other should say RED & third one should say PASS whenever 2 BLUE hats are seen. Same logic to be followed in case of 1 RED and  1 BLUE hats seen. But while doing this, we need to make sure responses are well distributed & not repeated by single member of team (See table below).