Geometrical Puzzle

Find the area of the shaded region.

Escape to the answer! 


Source 

Geometrical Puzzle - Solution

What was the puzzle?

Let's draw a line from each of vertex to the point at which all 4 regions intersect. This divides the given area into 2 triangles as shown below.

Obviously, here A and A' have equal area as they both share same base QS and height OT. Similarly, the areas of B & B', areas of C & C' and areas of D & D' must be equal. 

Rewriting, A = A', B = B', C = C' and D = D'.

 
Now rewriting respective areas,

It's clear that,

A + B = 32

C + D = 16

Adding above 2 equations gives, 

A + B + C + D = 32 + 16 = 48

But from figure, B + C = 20,

A + 20 + D = 48

A + D = 28.

That's the area of the shaded region which is equal to 28 Sq.cm

"What's The Area of The Triangle?"

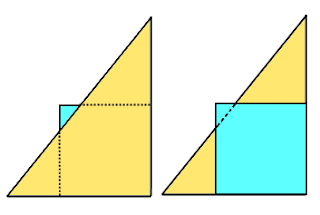
If I place a 6 cm × 6 cm square on a triangle, I can cover up to 60% of the triangle. If I place the triangle on the square, I can cover up to 2/3 of the square. What is the area, in cm², of the triangle?

(a) 22 4/5
(b) 24
(c) 36
(d) 40
(e) 60

Here is that mathematical calculation!

Calculation of Area of Triangle

What was the question?

The most important thing to note here is the area that square overlaps on the triangle is equal to the area that triangle overlaps the square with the maximum contact area. That is both the areas are supposed to be equal in amount. 


So if T is the area of the triangle & S is area of the square then,

0.6 T = 2/3  x S = 2/3 x (6x6) = 2/3 x 36 = 24

T = 40 Square cm.

Hence, answer is option (d) 40. 
 

Cut The Blue Cube Puzzle

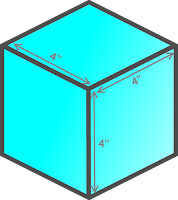
A solid, four-inch cube of wood is coated with blue paint on all six sides.

Then the cube is cut into smaller one-inch cubes. These new one-inch cubes will have either three blue sides, two blue sides, one blue side, or no blue sides. How many of each will there be?

Here is solution of the puzzle! 

Cut The Blue Cube Puzzle : Solution

What is the puzzle?

Apart from the 8 cubes at the center all 4 x 4 x 4 - 8 = 56 will have some paint on ones side at least. See below the 1/4 th cube is taken out.

The cubes at the 8 corners will have blue paint on three sides.

The cubes between corner cubes along 12 edges of big cube will have 2 sides painted. That is 12 x 2 = 24 cubes will painted with blue on 2 sides.

And 4 center cubes on each of 6 faces (left, right, top, bottom, front, back) will have only 1 side painted with blue. That is , there are 6 x 4 = 24 cubes having paint on one side only.

To conclude, out of 56 painted cubes,

24 cubes have paint on 1 side,

24 cubes painted with 2 sides,

8 are painted with three sides.

A Fractional Pink Shade

What fraction of this figure is shaded with the pink color?

Get the answer here!


Author : Ed Southall of Solve My Maths

Area Of A Fractional Pink Shade

A look at the question first!

Let's first recall the formula for the calculation of area of a triangle.

Area of triangle =  1/2 x Base x Height

Let's assume the side of the square is 1.

Now the triangle with the pink shade & triangle opposite to it are similar triangles. Similar triangles are triangle whose sides are in proportion with each other.

Since here base of pink triangle is double of un shaded opposite triangle, the height of pink triangle must be double of that smaller triangle.

But together, heights of both triangles must be equal to side of the square i.e. 1.

And hence, height of smaller triangle must be 1/3 & that of pink 2/3. (h + 2h = 3 ; h = 1/3).

So,

Area of Pink Triangle = 1/2 x Base x Height = 1/2 x 1 x 2/3 = 1/3.

So the area of pink shaded part is 1/3rd of total area occupied by square.



 

Connect Dots with Straight Lines

Can you connect all nine dots with only four straight lines without losing contact with the paper while drawing? 

Read here how it can be done!

Source 
 

Connected Dots With Straight Lines

What was the challenge? 

This question often asked in personality development training courses. It needs some out of box thinking. In the question, no where it is mentioned that you line can't go beyond 3 dots. But our brain assumes that & try to find the solution according to that only!