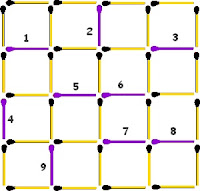
40 Matchsticks Challenge!

The diagram below shows 40 matchsticks arranged in a square grid.

What is the fewest number of matchsticks that need to be removed so that there are no squares (of any size) remaining?


This is how it can be done! 

Eliminating Square in 40 Matchsticks Challenge!

What was the challenge?

All that we need to do is that remove these differently colored 9 matchsticks.

So we get, 

There can be other variations of this answer but we have to remove 9 matchsticks at least to make sure there is no square.

Plan an Unbeatable Strategy

Two people play a game of NIM. There are 100 matches on a table, and the players take turns picking 1 to 5 sticks at a time. The person who takes the last stick wins the game. (Both players has to make sure that the winner would be picking only 1 stick at the end) 

Who has a winning strategy?

And what must be winning strategy in the person who takes the last stick looses?

This could be the winning strategy! 

Planned The Unbeatable Strategy!

What is the game?

The first person can plan an unbeatable winning strategy.

CASE 1 : The person picking last stick is winner.

All that he has to do is pick 4 sticks straightaway at the start leaving behind 96 stick. Then, he has to make sure that the count of remaining stick will be always divisible by 6 like 96, 90, 84, 78......6. 

So if the opponent takes away 2 sticks in his first turn, then first person has to take 6 - 2 = 4 sticks leaving behind 90 sticks there. That is if the opponent takes away X stick the first person need to pick 6 - X sticks.

Now, when there are 6 stick left, even if opponent takes away 5 sticks then 1 stick will be left for the first person.

And even if the opponent picks 4 sticks then first person will take 2 remaining sticks.

CASE 2 : The person picking last stick is looser. 

Now the first person need to take away 3 sticks in first turn leaving behind 97. Next, he has to make sure the count of remaining sticks reduced by 6 after each of his turn. That is, the count should be like 91,85,79,72......7.

So if the opponent takes away 4 sticks in his first turn, then first person has to take 6 - 4 = 2 sticks leaving behind 91 sticks there. That is if the opponent takes away X stick the first person need to pick 6 - X sticks.

When there are 7 sticks are left then even if the opponent takes away 5 sticks then first person can force him to pick the last stick by picking only 1 stick of remaining 2. 

And if the opponent takes away 4 sticks at this stage, the first person still can force him to pick last stick by picking 2 of remaining 3 sticks.

Conclusion : The first person always has a chance to plan a winning strategy.

Flip The Orientation of the Group

Assume these matchsticks as fishes. Can you flip the positions of the fishes horizontally i.e. 1 at the leftmost position and 4 at the rightmost position. Condition is that you can move only 3 matchsticks.

That's how it can be done!

Flipping The Orientation of The Group

What was the task given?


All we need to do is just move these sticks as shown below.

Make 7 Using 5 !

In the given picture, you can see that there are two matchsticks that have been used to create five squares. You are allowed to move just two matchsticks and must form seven squares. You can't overlap the matches and you are not allowed to break them. Also, like you can see in the picture, all squares must be closed. 

That's how it can be done!

Steps to Make 7 from 5

What was the challenge?

All we need to do is to re place these 2 match sticks.

So we get,