Aliens Meeting on the Earth

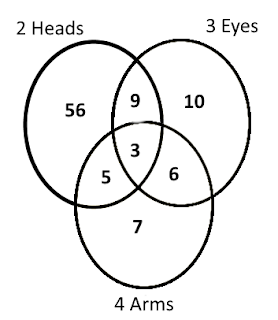
100 aliens attended an intergalactic meeting on earth.

73 had two heads,
28 had three eyes,
21 had four arms,
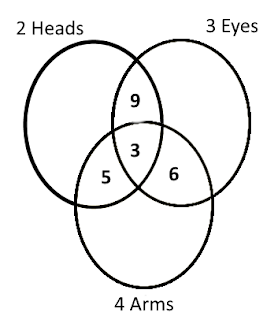
12 had two heads and three eyes,
9 had three eyes and four arms,
8 had two heads and four arms,
3 had all three unusual features.

How many aliens had none of these unusual features?

These are Aliens not having unusual features! 

Normal Aliens in the Meeting on the Earth

Read given data first!

Let's simplify the process with Venn diagram like below.

1. We know, 3 had all three unusual features.

2. 12 had two heads and three eyes, 9 had three eyes and four arms, 8 had two heads and four arms. Here, 3 having all unusual features too need to be counted in each of Aliens' counts above. 

So, Aliens having 2 unusual features of 2 heads & 3 eyes = 12 - 3 = 9.

Aliens having 2 unusual features of 3 eyes & 4 arms = 9 - 3 = 6.

Aliens having 2 unusual features of 2 heads & 4 arms = 8 - 3 = 5.

3. We know, 73 had two heads, 28 had three eyes, 21 had four arms.

Therefore, the number of Aliens having only 2 heads as an only unusual feature is 73 - (9 + 3 + 5) = 56.  

The number of Aliens having 3 eyes as an only unusual feature is 
28 - (9 + 3 + 6) = 10.

The number of Aliens having 4 arms as an only unusual feature is 
21 - (5 + 3 + 6) = 7.

4. So, we have 56 + 9 + 10 + 3 + 5 + 6 + 7 = 96 Aliens having at least one unusual feature. 

Therefore, the number of Aliens not having any of unusual features is 
100 - 96 = 4.

Language Barrier in International Meeting

Of the 1985 people attending an international meeting, no one speaks more than five languages, and in any subset of three attendees, at least two speak a common language. Prove that some language is spoken by at least 200 of the attendees.

Here is the proof! 

For The Communication in International Meeting

What was the barrier in the communication?

For any attendee A and B, having no common language there must be C who know the language of either A or B to form a trio as mentioned.

Let's make assumption contradicting the statement made in question. Suppose there are only 198 people who can talk in particular language with A or B. Since A can communicate in 5 languages, there are 5 x 198 = 990 people who can talk with A.

That is 990 people are there who have sharing 1 common language with 1 of 5 languages known by A. Similarly, B also can communicate with 990 more people.

Now, if A and B have no common language then there are only 990 + 990 = 1980 people having potential to become C in the trio. This obviously doesn't cover total of remaining people i.e. 1985 - 2 (A and B) = 1983.

Hence, our assumption goes wrong there. So there must be at least 200 attendees knowing the same language .