A New Word Every Day!
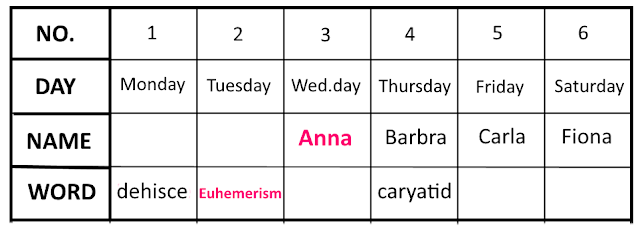
During a six-day period from Monday through Saturday, Eliza Pseudonym
and her friends Anna, Barbra, Carla, Delilah, and Fiona have subscribed
to an internet mailing list that features a new word every day.
No two women subscribed on the same day. On each day during the six-day period, a different word has been featured (abulia, betise, caryatid, dehisce, euhemerism, and floruit, in some order).
From the clues below, determine the day on which each woman subscribed, and the day on which each word was featured.
1. Exactly one of the women has a name beginning with the same letter of the alphabet as the word featured on the day that she subscribed to the mailing list.
2. The word "caryatid" was featured precisely two days prior to Fiona joining the mailing list.
3. Carla joined the mailing list on Friday.
4. Anna signed up for the mailing list precisely one day after the word "euhemerism" was highlighted.
5. Wednesday's word did not end with the letter "e".
6. Barbra subscribed precisely three days after the word "dehisce" was featured.
Here is every word of woman of the day!
No two women subscribed on the same day. On each day during the six-day period, a different word has been featured (abulia, betise, caryatid, dehisce, euhemerism, and floruit, in some order).
From the clues below, determine the day on which each woman subscribed, and the day on which each word was featured.
1. Exactly one of the women has a name beginning with the same letter of the alphabet as the word featured on the day that she subscribed to the mailing list.
2. The word "caryatid" was featured precisely two days prior to Fiona joining the mailing list.
3. Carla joined the mailing list on Friday.
4. Anna signed up for the mailing list precisely one day after the word "euhemerism" was highlighted.
5. Wednesday's word did not end with the letter "e".
6. Barbra subscribed precisely three days after the word "dehisce" was featured.
Here is every word of woman of the day!