The Little Johnny's Dilemma

Little Johnny is walking home. He has $300 he has to bring home to his mom. While he is walking a man stops him and gives him a chance to double his money. 

The man says -

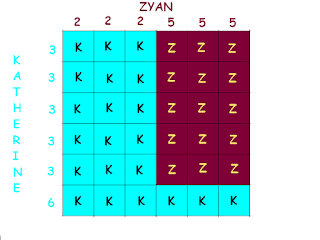
 "I'll give you $600 if you can roll 1 die and get a 4 or above, you can roll 2 dice and get a 5 or 6 on at least one of them, or you can roll 3 dice and get a 6 on at least on die. If you don't I get your $300."
 
What does Johnny do to have the best chance of getting home with the money?

THIS is the BEST he can do! 

The Loss Making Deal !

What was the deal?


The little Johnny should not accept the deal.

The problem is actually finding the probability of winning in each case dice throw.

---------------------------------------------

CASE 1 :  

Condition - Roll a die and get 4 or above.

The probability in the case is 3/6 = 1/2 (getting 4,5,6 from 6 possible outcomes). 

That is only 50% chances of winning the deal.

---------------------------------------------

CASE 2 :

Condition - Roll 2 dice and a 5 or 6 on at least one of them.

Let's find the probability that none get a 5 or 6. 

Probability that single die doesn't get a 5 or 6 is 4/6 = 2/3 by getting 1,2,3,4 in possible 6 outcomes.

Since, these 2 results are independent, the probability that neither dice gets a 5 or 6 is 2/3 x 2/3 = 4/9.

So, the probability that at least one of them gets a 5 or 6 is 1 - 4/9 = 5/9.

That is, about 56% chances of winning the deal.

By other approach, there are 36 possible combinations in 2 dice throw.

(1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6)

(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)

(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)

(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)

(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)

(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6) 

There are total 20 combinations (last 2 rows and 2 columns) where at least one die gets a 5 or 6.

Hence, the probability in the case is 20/36 = 5/9 i.e. about 56% of winning chances.

----------------------------------------

CASE 3 : 

Condition - Roll three dice and get a 6 on at least on die.  

Again finding probability that none gets a 6.

Probability that single die doesn't get a 6 is 5/6 by getting 1,2,3,4,5 out of 6 possible outcomes.

Hence, the probability that three dices doesn't get a 6 = 5/6 x 5/6 x 5/6 = 125/216.

Then the probability that at least one of them get a 6 = 1 - 125/216 = 91/216 

That is only 42% chances of winning the deal.

--------------------------------------------

On the other hand Johnny can be 100% sure that he will take $300 to home if he doesn't accept the man's deal. 

Bags of Marbles - Puzzle

There are three bags, each containing two marbles. Bag A contains two white marbles, Bag B contains two black marbles, and Bag C contains one white marble and one black marble. 

You pick a random bag and take out one marble, which is white. 

What is the probability that the remaining marble from the same bag is also white?

Here is the solution! 

Bags of Marbles Puzzle - Solution

What is the puzzle?

Well, the probability that the second marble is also white should be 1/2 not 2/3 as most of answers to this puzzle claims!

There is no way that you have picked up the bag B having 2 black marbles since the first marble you have drawn is white. Hence, you must have picked up Bag A or C.

Claim :  

You chose Bag A, first white marble. The other marble will be white

You chose Bag A, second white marble. The other marble will be white

You chose Bag C, the white marble. The other marble will be black

So 2 out of 3 possibilities are white.


Hence, 2/3 is the probability of the second ball is also white.


Correct Approach :

The probability of the particular bag being picked randomly is 1/3 initially. Once the bag picked and since the marble drawn from it is white, the bag must be either A (2 whites) or C (1 white, 1 black).

The probability that the bag you picked is A (or C) must be 1/2 and hence the probability that second marble is also white (or not white) has to be also 1/2.

Flipping The Unusual Coins

You have three coins. One always comes up heads, one always comes up tails, and one is just a regular coin (has equal change of heads or tails). If you pick one of the coins randomly and flip it twice and get heads twice, what is the chance of flipping heads again?

Chances of flipping head again are - .......% Click to know!

Chance of Flipping Head Again

What was the problem?

For a coin to always show head on flip we assume both it's sides are heads and the coin which is showing tail always we assume both of it's sides are tails.

There is no way that you have selected tail only coin since there are 2 heads in first 2 flips.

So it could be either head only coin say D coin or regular fair coin say F.

Let H1 and H2 be the sides of head coin and H, T are side of fair coin.

If it's head only coin D, then possible scenarios on 2 flips are -

DH1 DH1
DH1 DH2
DH2 DH1
DH2 DH2

And if it's fair coin F then possible scenarios on 2 flips are -

FH FH
FH FT
FT FH
FT FT

There are total five combinations (all 4 of head coin + first one of fair coin) where there are 2 consecutive heads on 2 flips.

So, the chances that you have picked a head coin is (4/5) and that you picked fair coin is (1/5).

For head coin, the probability of getting head again is 1 and that for fair coin is (1/2).

Since you holding either head coin or fair coin,

Probability (Head on third flip) = 
Probability (You picked Head coin) x Probability (Head on head coin) + Probability (You picked fair coin) x Probability (Head on fair coin) 


Probability (Head on third flip) = (4/5) x 1 + (1/5) x (1/2)

Probability (Head on third flip) = 9/10.

Hence, the chance of flipping head again on third flip is 90%.

Probability of The Correct Answer?

This is a popular probability puzzle in which you have to select the correct answer at random from the four options below.

Can you tell, whats the probability of choosing correct answer in this random manner.

1) 1/4
2) 1/2
3) 1
4) 1/4

And the correct answer is......

Finding The Probability of Correct Answer

What was the question?

It can't be 1/4 as 1/4 appears 2 times in given 4 options as probability of correct answer when random selection of option in that case would be 2/4 = 1/2. This will be contradiction.

It can't be 1/2 either since the probability of the 1 correct answer out of 4 available options on random selection would be 1/4. That will be contradiction again.

It can't be 1 too as again probability of the 1 correct answer out of 4 available options on random selection would be 1/4. Once again this is contradiction.

Hence, the probability of the 1 correct answer out of 4 available options on random selection would be 0.

Avoid The Collision of Ants

Three ants are sitting at the three corners of an equilateral triangle. Each ant starts randomly picks a direction and starts to move along the edge of the triangle. What is the probability that none of the ants collide?

'THIS' is the probability!

To Avoid The Collision of Ants

What was the problem?

Each ant can decide to go either clockwise or anti-clockwise. That is there are 2 options available for each ant to go. Hence, there will be total 2x2x2 = 8 possible combination of ants' different paths.

Now 2 ants won't collide if & only if all are either moving clockwise or anti-clockwise. In short, out of 8 possible combinations only 2 combinations are there where ants won't collide.

Hence, the probability that ant won't collide is 2/8 = 0.25.  

Case of 3 Identical Notebooks

Three people all set down their identical notebooks on a table. On the way out, they each randomly pick up one of the notebooks. What is the probability that none of the three people pick up the notebook that they started with?

That's correct probability!

Probability in Case of 3 Identical Notebooks

What was the case?

Let's name peoples as Person - 1, Person - 2, Person - 3 and their notebooks as Notebook - 1, Notebook - 2 and Notebook 3 respectively.

Now there can be 6 ways 3 notebooks can be distributed among 3 persons like below.

(Here, for convenience, 3 different colors are assigned to the notebooks of 3 persons.)

As we can see, there are only 2 cases, where the each of person not getting own notebook. In rest of cases, at least 1 person got own notebook & notebooks of others are shuffled between 2.

So the probability that none of the three people pick up the notebook that they started with is 2/6 = 1/3. 

Unfair Game of Strange dice

Katherine and Zyan are playing a game using strange dice. Each die is a cube with six sides. Katherine's die has sides numbered 3, 3, 3, 3, 3, and 6. Zyan's die has sides numbered 2, 2, 2, 5, 5, and 5.

To play the game, Katherine and Zyan roll their dice at the same time and whoever rolls the higher value wins. If they play many times, who will win more frequently, Katherine or Zyan?

This person will be winning more! 
 

Advantage in Unfair Game of Strange Dice

What was the game?

Shortest Way : 

Katherine's die has sides numbered 3, 3, 3, 3, 3, and 6. And Zyan's die has sides numbered 2, 2, 2, 5, 5, and 5. That means whenever Zyan rolls a 2 then Katherine will always win. The probability that Zyan rolls 2 is 3/6 = 1/2. So in half of the cases, the Katherine will be winner of the game. Moreover, whenever, Zyan rolls a 5, Katherine can win if she rolls a 6. In short, in more than half cases, Katherine will win hence she has more advantage in this game.


Precise Way : 

Katherine will win if

1. Zyan rolls a 2 with probability 3/6 = 1/2

2. Zyan rolls a 5 (probability 3/6 = 1/2) and Katherine rolls a 6 (probability 1/6). So the probability for this win = 1/12.

Hence, Katherine has got 1/2 + 1/12 = 7/12 chances of winning.

Zyan will win if he rolls a 5 (probability 1/2) and Katherine rolls a 3 (probability 5/6) with probability = 1/2 x 5/6 = 5/12.  

That proves, Katherine has more chances (7/12 vs 5/12) of winning this game. 

Another Way : 

There can be 36 possible cases of numbers of cubes out of which in 15 cases Zyan seems to be winning and in 21 cases, Katherine is winning. Again, Katherine having more chances of winning (21/36 = 7/12) than Zyan (15/36 = 5/12). 

The Tuesday Birthday Problem

I ask people at random if they have two children and also if one is a boy born on a Tuesday. After a long search I finally find someone who answers yes. What is the probability that this person has two boys? Assume an equal chance of giving birth to either sex and an equal chance to giving birth on any day.

Tip: Don't conclude too early. 

Click here to know the correct answer! 

Finding The Correct Probability

How tricky it was?

If you think that the probability is 1/2 after reading that the couple has equal chance of having child of either sex then you are in wrong direction.

Take a look at the table below.

There are 27 possible combinations when boy is born on Tuesday. Out of which there are only 13 possible combinations where either boy (first or second) is born on Tuesday. 

Hence the probability that the person having at least 1 boy off his 2 boys born on Tuesday is 13/27.

Probability of Correct Package Labeling

Brad Doe works for a packaging company. One day, he received four separate orders and accidentally mixed up the addresses, so he applied the
address labels at random. 

What is the probability that exactly three packages were correctly labeled?

Labeled Packages

 Skip to answer! 

Common Sense in Finding Probability

Why this question?

Answer is 1!

If three are correctly placed fourth has to be. There are only 4!