The Antisocial Club Challenge

The Antisocial Club meets every week at Jim's Bar. Since they are so antisocial, however, everyone always sits as far as possible from the other members, and no one ever sits right next to another member. Because of this, the 25-stool bar is almost always less than half full and unfortunately for Jim the members that don't sit at the bar don't order any drinks. 

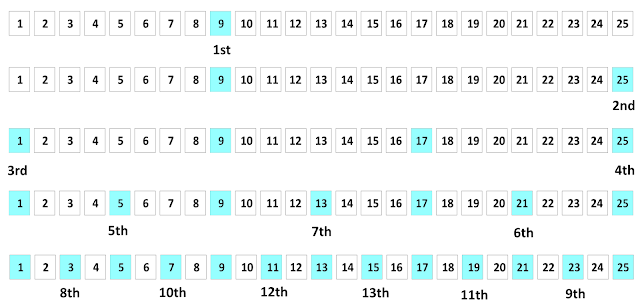
Jim, however, is pretty smart and makes up a new rule: The first person to sit at the bar has to sit at one of two particular stools. If this happens, then the maximum number of members will sit at the bar. 

Which stools must be chosen? Assume the stools are numbered 1 to 25 and are arranged in a straight line.

Wise Selection of first 2 Seats made available! 

Logical Response to The Antisocial Club Challenge

What was the challenge?

The bar owner Jim put only 2 options for first person to seat and those options are Stool No. 9 and Stool No.17. We'll call seat for stool for convenience.

Choice of numbers 9 and 17 is because of symmetry explained below.

Suppose the first person choose seat no.9.

Then the second person has to choose the furthest seat i.e. seat no.25.

The third person will choose seat no.1 which is furthest from seat no.9 and 25.

The fourth person won't have option other than seat no.25 which is the furthest from rest of 3.

For the fifth person, seats numbered 5, 13 and 21 are available which are equidistant from 2 persons. We assume he chooses farthest from the seat occupied by person who entered just ahead of him. That is he chooses seat no.5.

Since, seat no.21 is furthest from seat no.5 and only seat equidistant from 17 & 25, the sixth person will choose seat no.21.

With that, 7th person won't have any option other than seat no.13 to maintain distance from others.

With the same logic, next 6 persons occupies seat numbered 3, 23, 7, 19, 11, 15.

So there will be 13 people maximum in the bar with no one seating next to each other.

The same seat numbers will be occupied even if the first person choose seat no.17. The second person will choose seat no.1, third will choose seat no.25, fourth will choose seat no.9 and so on.

But if the first person doesn't choose 9 or 17 then there can be less than or equal to 12 people maximum in the bar following their antisocial trait.

The Allotment Challenge?

Five bankers are sharing 12 golden ingots. They decide to proceed that way : 

The elder one will suggest an ingots allotment. The rest will vote for or against it. If the majority accepts, the sharing is ratified. If not, the elder will be dismissed. So, the sharing would be done between the remaining banker with the same rules. 

Knowing that they are set from left to right in a diminishing order of their ages, how would be the allotment ?

THIS should be the UNDENIABLE Allotment!

Source 

The Undenial Allotment Proposition!

What were rules of allotment process?

The eldest should allot ingot like 9, 0, 1, 0, 2 among 5 bankers.

Let's name bankers as Banker 5, Banker 4 ...... Banker 1 according to decreasing order of their ages.

------------------------------------------------------------------------------

CASE 1 : 

Suppose there are only 2 bankers left then the youngest will always deny whatever elder offers so that he can take away all 12 ingots on his turn.

------------------------------------------------------------------------------

CASE 2 : 

If case is reduced to 3 bankers then the eldest knows that the youngest is not going to agree with him in any case. With that, the eldest will be dismissed and case reduced to CASE 1 where youngest can take away all. 

So, the eldest here proposes allotment as 11, 1, 0. The Banker 2 has no option than to accept this proposal otherwise he won't get anything if case is reduced to 2 bankers as in CASE 1 above.

------------------------------------------------------------------------------

CASE 3 : 

With 4 bankers, the eldest would propose allotment 9, 0, 2, 1.

In the case, Banker 3 will never accept any proposal as after banker 4 is dismissed he would be getting 11 ingots as in CASE 2 above.

The Banker 2 will happily agree with the eldest as he would be getting 1 more ingot than the CASE 2. 

And Banker 1 knows he will be getting nothing if the case is reduced to 3 bankers as in CASE 2. So, he too will agree with the eldest in the case.

------------------------------------------------------------------------------

CASE 4 : 

With 5 bankers, the eldest i.e. Banker 5 should propose allotment 9,0,1,0,2.

Obviously, any how Banker 4 is going to deny any proposal as he wants the distribution among 4 bankers where he will be getting 9 ingots as in CASE 3 above. 

And if Banker 5 is eliminated and the case is reduced to CASE 3 where 4 bankers are left then Banker 3 knows he won't be getting anything. So, better he should be happily agree this proposition where he is getting at least 1 ingot.

Finally, offering Banker 5 one more extra ingot than the case where 4 bankers will be left, makes him in favor of this proposition.

Notice that the Banker 5 has to give 3 ingots at least to banker 2 to get his vote as he will be getting 2 ingots in case of 4 bankers as in CASE 3. Whereas, in the same case Banker 3 is not getting anything & would be happily agree if getting 1 ingot at least in this case. 


------------------------------------------------------------------------------

 

Four Glasses Puzzle

Four glasses are placed on the corners of a square table. Some of the glasses are upright (up) and some upside-down (down). A blindfolded person is seated next to the table and is required to re-arrange the glasses so that they are all up or all down, either arrangement being acceptable, which will be signaled by the ringing of a bell. 

The glasses may be re-arranged in turns subject to the following rules. 

1.Any two glasses may be inspected in one turn and after feeling their orientation the person may reverse the orientation of either, neither or both glasses.

2.After each turn the table is rotated through a random angle. 

3.The puzzle is to devise an algorithm which allows the blindfolded person to ensure that all glasses have the same orientation (either up or down) in a finite number of turns. The algorithm must be non-stochastic i.e. it must not depend on luck.

Here is that algorithm!

Solution of Blind Bartender's Problem

What was the puzzle?

Below is the algorithm which makes sure the bell will ring in at most five turns.

1.On the first turn choose a diagonally opposite pair of glasses and turn both glasses up.
At this point, the position of other 2 glasses is not known.

2.On the second turn, choose 2 adjacent glasses. One of them was turned up in the previous step, so other may or may not in up position. If the other is down then turn it up and if remaining one X is also in up position then bell will be rung.

If the bell does not ring then there are now three glasses up and one down(3U and 1D).

3.On the third turn choose a diagonally opposite pair of glasses. If one is down, turn it up and the bell will ring.

And if you find both are up, then you must have chosen other diagonally opposite pair.

If so, then turn one down so that 2 glasses are up and other 2 are down.

4.On the fourth turn choose two adjacent glasses and reverse both. If both were in the same orientation then the bell will ring. 

And in case, if you find one is up and other down like -

still reverse orientation of both as - 

Now diagonally opposite pairs are either up or down.

5.On the fifth turn choose a diagonally opposite pair of glasses and reverse both.

The bell will ring for sure.