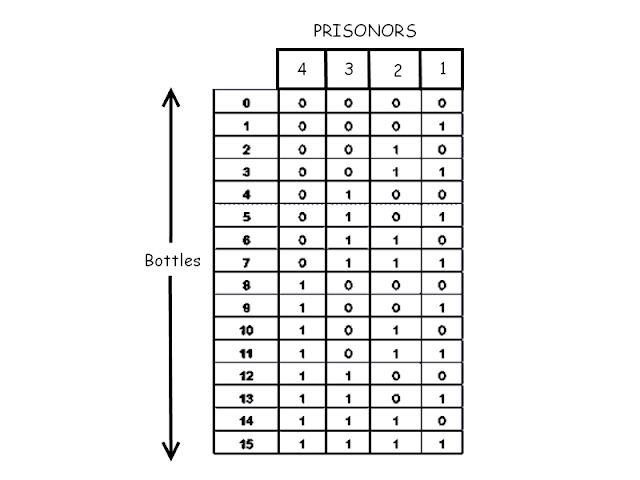
Test Of Poison

You are the ruler of a medieval empire and you are about to have a celebration tomorrow. The celebration is the most important party you have ever hosted. You've got 1000 bottles of wine you were planning to open for the celebration, but you find out that one of them is poisoned.

The poison exhibits no symptoms until death. Death occurs within ten to twenty hours after consuming even the minutest amount of poison.

You have over a thousand slaves at your disposal and just under 24 hours to determine which single bottle is poisoned.

You have a handful of prisoners about to be executed, and it would mar your celebration to have anyone else killed.

What is the smallest number of prisoners you must have to drink from the bottles to be absolutely sure to find the poisoned bottle within 24 hours? 

Here is the test designed for it! 

Source 

Test To Detect The Poison

Here is the challenge for us! 

Here binary number system can come to rescue. Just for a  moment, let's assume there are 15 bottles. Now let's number the bottles from 1 to 15. To test these 15 bottles we need 4 prisoners as below. Let's number the prisoners from in descending 4 to 1.

Wherever 1 is written for the particular bottle number, that bottle should be given to particular prisoner. Otherwise should not.

So for the specific bottle with unique number a specific combination of prisoners (they are bits here) would be formed. 

For example, if bottle labeled as 11 has a poison then prisoner no. 4,2,1 would die. In other words, if prisoner 4 & 2 die then the bottle no. 10 had poison.

For 16th bottle we would have needed 1 more prisoner.

In similar way, to test 1000 bottles, we need 10 prisoners (2^10=1024). Depending on what combination of prisoner die we can determine which bottle had poison. If prisoners numbered from 10 to 1 & if prisoner 10,8,6,3 & 2 die then bottle no.678 (binary - 1010100110) must had poison. Since the poison takes some time to take effect, even if prisoners taste this bottle, we still would have time to test rest of all bottles in given binary pattern. 

  Poisonous Bottle

In case there were 1025 bottle, we would have needed 11 prisoners.