The Thanksgiving Pageant

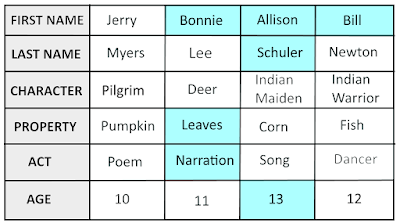
Allison, Jerry, Bonnie, and Bill are participating in a Thanksgiving Pageant at their school. 

The students will portray an Indian warrior, a pilgrim, an Indian maiden, and a deer. Their props consist of a pumpkin, a fish, a basket of corn, and colored leaves. During the pageant, they will recite a poem, sing a song, do a dance, and act as the narrator. Their parents, whose lasts names are Lee, Newton, Myers, and Schuler, will be watching in the audience. The ages of the performers are 13, 12, 11, and 10 years old. 

Use the clues to help you find out who will be doing what for the pageant.

1. Mrs. Lee made her daughter's costume and also the costumes of the Indian maiden and the dancer. 

2. Mr. Myers helped his son rehearse his poem. 

3. The dancer was older than Lee and the pilgrim, but younger than Allison. 

4. The 11-year-old ripped her deer outfit, but her mother pinned it.

5. Newton carried his fish during his tribal dance.

6. Jerry's pumpkin was a symbol of the feast for the pilgrims. 

7. The Indian maiden carried corn as she sang the song of feasting.

Simplified Solution Here! 

Little Performers at The Thanksgiving Pageant

What was the puzzle?

Given Data : 

STUDENTS     : Allison, Jerry, Bonnie, Bill

CHARACTERS : Indian warrior, Pilgrim, Indian maiden, Deer

PROPS           : Pumpkin, Fish, Basket of corn, Colored leaves

ACT                : Poem, Song, Dance, Narrator

LAST NAMES  : Lee, Newton, Myers, Schuler

AGE                : 13, 12, 11, 10

Given Clues : 

1. Mrs. Lee made her daughter's costume and also the costumes of the Indian maiden and the dancer. 

2. Mr. Myers helped his son rehearse his poem. 

3. The dancer was older than Lee and the pilgrim, but younger than Allison. 

4. The 11-year-old ripped her deer outfit, but her mother pinned it.

5. Newton carried his fish during his tribal dance.

6. Jerry's pumpkin was a symbol of the feast for the pilgrims. 

7. The Indian maiden carried corn as she sang the song of feasting.

STEPS :

First of all let's make a table like below & fill it as per clues.

1]  As per clue (1), student having last name Lee, an Indian maiden and dancer are three different students.

2] As per (3), the dancer must be 12 years old with Lee and Pilgrim having age 10 & 11 but order yet to be known. With that Allison must be 13 years old. This clue also suggests that the dancer or Lee isn't pilgrim.

3] The clue (5) clearly suggest that Newton is dancer carrying fish as a property. Also, clue (6) suggests Jerry is pilgrim having pumpkin. And clue (7) suggests that, Indian Maiden sung a song while carrying a basket of corn.

4] With that, we can conclude that Lee must be carrying colored leaves. Also, the clue (4) must be pointing at Lee now. So Lee is 11 years old wearing deer outfit.

5] It's clear now that Newton is Indian Warrior. And, 10 years old (STEP 2) Jerry is Myers who father helped him to rehearse his poem as per clue (2).

6] Since Allison is 13 years old, she must be Indian Maiden carrying a basket of corn while singing a song. She must have last name Schuler - the only last name left. Since (1) suggests Lee is girl, her name must be Bonnie who is narrator carrying a colored leaves. Finally, first name of Newton must be Bill.

7] So, the final table looks as - 

Story of Four High School Friends

Four high school friends, one named Cathy, were about to go to college. Their last names were Williams, Burbank, Collins, and Gunderson. Each enrolled in a different college, one of them being a state college. 

From the clues below determine each person's full name, and the college he or she attended.

1. No student's first name begins with the first letter as her or his last name, and no students first name's last letter is the same as his last name's last letter.

2. Neither Hank or Williams went to the community college.

3. Alan, Collins, and the student who went to the university all lived on the same street. The other student lived two blocks away.

4. Gladys and Hank lived next door to each other.

5. The private college accepted Hank's application, but he decided he could not afford to go there.

Here is ANALYSIS of the story! 

Analysing The Story of Four High School Friends

What was the story?

GIVEN DATA : 

First Name : Hank, Gladys, Cathy, Alan 
Last Name : Collins, Burbank, Gunderson, Williams 
College       :  State College, University, Community College, Private College 

HINTS : 

1. No student's first name begins with the first letter as her or his last name, and no students first name's last letter is the same as his last name's last letter.

2. Neither Hank or Williams went to the community college.

3. Alan, Collins, and the student who went to the university all lived on the same street. The other student lived two blocks away.

4. Gladys and Hank lived next door to each other.

5. The private college accepted Hank's application, but he decided he could not afford to go there.   

STEPS :  

1] Let's make a table like below and fill it as per hints.

  
2] As per Hint (3), we have, Alan, Collins and student going to the university as 3 different students.

3] As per (1), Collins can't be Cathy & as per (4), Cathy can't be at no.3 as in that case no blocks will be left for (4) to be true. Hence Cathy must be at no.4.

4] As per (2), Hank and Williams are two different students. And as per (4), Gladys and Hank must be at 2 & 3 (and anyhow these are only blocks left for them) but order yet to be known. So, Williams is certainly not at 3 or 2. And as per (1), Gladys can't be Gunderson or Collins or Williams & Hank can't be Burbank.  Therefore, Hank must be Collins at 2 and Gladys must be Burbank at 3.

5] Now, as per (1), Alan can't be Gunderson hence must be Williams and Cathy must be Gunderson. 

6] As per (2), neither Hank nor Williams went to community college, hence Cathy Gunderson must be. And as per (5), Hank didn't choose private college hence must have chosen state college while Alan Williams must be in private college.

7] Therefore, the final table looks like as below.

 

The Numbered Hats Test!

One teacher decided to test three of his students, Frank, Gary and Henry. The teacher took three hats, wrote on each hat an integer number greater than 0, and put the hats on the heads of the students. Each student could see the numbers written on the hats of the other two students but not the number written on his own hat.

The teacher said that one of the numbers is sum of the other two and started asking the students:

— Frank, do you know the number on your hat?

— No, I don’t.

— Gary, do you know the number on your hat?

— No, I don’t.

— Henry, do you know the number on your hat?

— No, I don’t.

Then the teacher started another round of questioning:

— Frank, do you know the number on your hat?

— No, I don’t.

— Gary, do you know the number on your hat?

— No, I don’t.

— Henry, do you know the number on your hat?

— Yes, it is 144.

What were the numbers which the teacher wrote on the hats?

Here are the other numbers!

Source 

Cracking Down The Numbered Hats Test

What was the test?

Even before the teacher starts asking, the student must have realized 2 facts.

1. In order to identify numbers in this case, the numbers on the hats has to be in proportion i.e. multiples of other(s). Like if one has x then other must have 2x,3x etc.

2. Two hats can't have the same number say x as in that case third student can easily guess the own number as 2x since x-x = 0 is not allowed.

--------------------------------------------------------------------------------------------------

Now, if numbers on the hats were distributed as x, 2x, 3x then the student wearing hat of number 3x would have quickly responded with correct guess. That's because he can see 2 number as x and 2x on others hats and he can conclude his number as x + 2x = 3x since 
2x - x = x is invalid combination (x, x, 2x) where 2 numbers are equal.

Other way, he can think that the student with hat 2x would have guessed own number correctly if I had x on my own hat. Hence, he may conclude that the number on his hat must be 3x.

But in the case, all responded negatively in the first round of questioning. So x, 2x, 3x combination is eliminated after first round.

-------------------------------------------------------------------------------------------------- 

That means it could be x, 3x, 4x combination of numbers on the hats.

In second round of questioning, Henry guessed his number correctly.

If he had seen 3x and 4x on other 2 hats then he wouldn't have been sure with his number whether it is x or 7x.

Similarly, he must not have seen x and 4x as in that case as well he couldn't have concluded whether his number is either 5x or 3x.

But when he sees x and 3x on other hats he can tell that his number must be 4x as 2x (x,2x,3x combination) is eliminated in previous round!

So Henry can conclude that his number must be 4x.

Since, he said his number is 144,

4x = 144

x = 36

3x = 108.

Hence, the numbers are 36, 108, 144.

Who is Taller - A or B?

200 students are arranged in 10 rows of 20 children. The shortest student in each column is identified, and the tallest of these is marked A. The tallest student in each row is identified, and the shortest of these is marked B. If A and B are different people, which is taller?

This person will be taller in any case!

In Any Case B is Taller!

Why the height comparison?

 B will be always taller in any case.

Case 1 : If A and B are standing in the same row the obviously B is taller than A as B is tallest among all in that row.

Case 2 : If A and B are standing in the same column then still B is taller than A as A is shortest among all in that column.

Case 3 : If A and B are standing in different row and column then there must be somebody C which has same column as A and same row as B. This C is shorter than B (as B is tallest in row) and he is taller than A (as A is shortest in that column). That is B > C and C > A.

Hence, in any case, B is always taller than A. 

Locker Room & Strange Principal

A high school has a strange principal. On the first day, he has his students perform an odd opening day ceremony:

There are one thousand lockers and one thousand students in the school. The principal asks the first student to go to every locker and open it. Then he has asked the second student go to every second locker and close it. The third goes to every third locker and, if it is closed, he opens it, and if it is open, he closes it. The fourth student does this to every fourth locker, and so on. After the process is completed with the thousandth student, how many lockers are open?

What principal was trying to teach? 

Source 

The Lesson Taught By Strange Principal

Where it did begin? 

While finding the solution we need to keep basic fact from the problem in mind. Since lockers were closed initially, the lockers which are 'accessed' for odd number of times only are going to open. Rest of all would be closed.

Now task is to find how many such lockers are there which were 'accessed' for odd number of times.

Let's take any number say 24 for example, which is not perfect square & find out how many factors it has.

24 = 1 x 24
24 = 2 x 12
24 = 3 x 8
24 = 4 x 6

So factors are 1,2,3,4,6,8,12,24 i.e. 8 numbers as factors which is even number. Every factor is paired with other 'unique' number! So this pairing always makes number of factors 'even'. In the problem, this lock no.24 will be 'accessed' by 1st, 2nd, 3rd..................24th student. That means 'accessed' even number of time & hence would remain closed.

Now let's take a look at lock no. 16 in which 16 is perfect square. Finding it's factors,

16 = 1 x 16
16 = 2 x 8
16 = 4 x 4

we get 1,2,4,8,16 i.e. 5 numbers as factors which is odd. The reason behind is here 4 appears twice (with itself) while rest of others are paired with other 'unique' number. Hence, number of factors of a perfect square are always odd. Now here lock 16 would be accessed by 1st, 2nd, 4th, 8th, 16th i.e. 5 times. Hence it will be open.

Like this way, every lock with number which is perfect square would be 'accessed' for odd number of times & hence would remain open! e.g. 1,4,9,16,25,49 & so on.

Now 961 (31^2) is the maximum perfect square that can appear within 1000 (32^2) as 1024 goes beyond.

Hence there would be 31 locks open while rest of all closed!

Lesson Of The Day

So what lesson taught by strange principal? The number which is perfect square has odd number of divisors.