A Round Table Conference
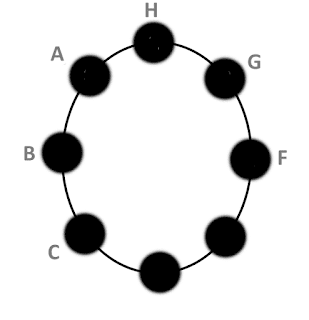
8 people have to be seated at a round banquet table. The seats are
number 1-8.
For this teaser, 5 is opposite 1, 6 is opposite 2 and so on. Likewise, "next to" means one of the neighboring seats only. i.e., 8 is next to 1 and 7.
A and H are the only French speaking people on the table. They need to be seated together.
B and F should sit opposite each other.
C, F, and G all know Russian, but don't necessarily need to sit next to each other. In fact, G wants to sit next to someone who knows French.
D is English and insists on sitting next to at least one other English speaking person, and pat opposite the good looking H. E is the only other English speaker in the group, but he wants to sit next to someone who knows Russian.
G agrees to sit next to F only on condition that the other side must have a French speaker. C does not sit next to either of them.
C however, agrees to sit next to B, who is the only Bavarian in the group.
A will not sit next to a Russian or an English speaker.
THIS should be the seating arrangement!
For this teaser, 5 is opposite 1, 6 is opposite 2 and so on. Likewise, "next to" means one of the neighboring seats only. i.e., 8 is next to 1 and 7.
A and H are the only French speaking people on the table. They need to be seated together.
B and F should sit opposite each other.
C, F, and G all know Russian, but don't necessarily need to sit next to each other. In fact, G wants to sit next to someone who knows French.
D is English and insists on sitting next to at least one other English speaking person, and pat opposite the good looking H. E is the only other English speaker in the group, but he wants to sit next to someone who knows Russian.
G agrees to sit next to F only on condition that the other side must have a French speaker. C does not sit next to either of them.
C however, agrees to sit next to B, who is the only Bavarian in the group.
A will not sit next to a Russian or an English speaker.
THIS should be the seating arrangement!