'Morning Melange' - Puzzle

This morning, the popular Bay area cable access TV show, "Morning Melange", featured six guests (including Francine and Evan). Each guest lives in a different town in the region (including Corte Madera), and each has a different talent or interest that was the focus of his or her segment. The segments began at 6:45, 7:00, 7:15, 7:30, 7:45 and 8:00. 

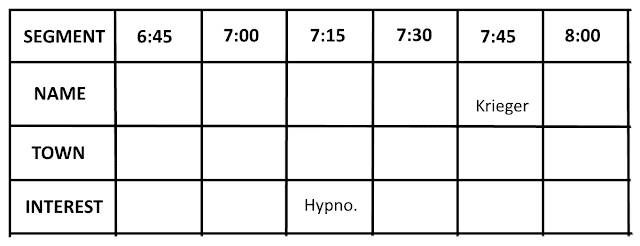
Discover, for each time, the full name of the featured guest, where he or she lives and his or her special interest.
 
1. The first three guests were, in some order: the person surnamed Ivens, the person from Berkeley and the antique car collector.

2. Damien's segment was sometime before Lautremont's segment.

3. Krieger's segment began at 7:45.

4. Alice appeared after the person from Oakland and before the person surnamed Morley.

5. The people from Berkeley and Daly City aren't of the same sex.

6. The six guests were: Cathy, the person whose first name is Damien, the person whose last name is Novak, the person from Daly City, the person from Palo Alto and the bungee jumper.

7. The last name of the financial adviser is either Lautremont or Novak.

8. Jaspersen's segment began exactly 45 minutes after the beekeeper's segment.

9. The crepe chef went on sometime before the person from Sausalito and sometime after Brandon.

10. The hypnotherapist's segment began at 7:15.

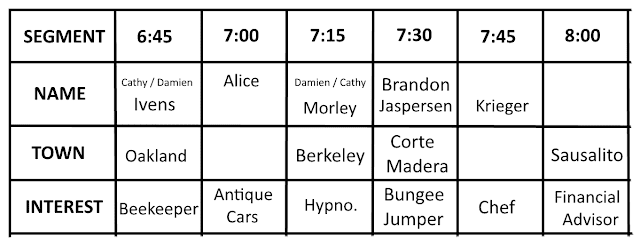
HERE is SOLUTION! 

'Morning Melgane' Puzzle - Solution

What was the puzzle?

Rewriting all the given clues once again.

--------------------------------------------------------------------------- 

1. The first three guests were, in some order: the person surnamed Ivens, the person from Berkeley and the antique car collector.

2. Damien's segment was sometime before Lautremont's segment.

3. Krieger's segment began at 7:45.

4. Alice appeared after the person from Oakland and before the person surnamed Morley.

5. The people from Berkeley and Daly City aren't of the same sex.

6. The six guests were: Cathy, the person whose first name is Damien, the person whose last name is Novak, the person from Daly City, the person from Palo Alto and the bungee jumper.

7. The last name of the financial adviser is either Lautremont or Novak.

8. Jaspersen's segment began exactly 45 minutes after the beekeeper's segment.

9. The crepe chef went on sometime before the person from Sausalito and sometime after Brandon.

10. The hypnotherapist's segment began at 7:15.

--------------------------------------------------------------------------- 


STEPS :

1] Let's make table like below for simplicity & easy understanding.

   
2] As per (10), hypnotherapist took segment starting at 7:15 & (3) suggest that Krieger started at 7:45.

3] As per (8), Jaspersen must be either at 7:30, 7:45 or 8:00 (i.e. in second half) while beekeeper must be at 6:45 or 7:00 or 7:15. But 7:15 segment is already occupied by hypnotherapist and Krieger is there already at 7:45.
So, Jaspersen can't be at 7:45. Hence, Jaspersen must be at 7:30 and beekeeper at 6:15 for (8) to be true.

With that, the antique car collector pointed by (1) must be at 6:45.

4] Since, as per (7), the financial adviser isn't Jaspersen or Kreiger ,therefore is on during the 8:00 segment. As per (4), Morley can't be in first 2 segments & as per (7) Morely is not a financial adviser. Thus, Morley needs to be at 7:15.

5] With that as (4) suggests, Alice must be on during segment started at 7:00 & person from Oakland took 6:45.

6] Now, as (1) suggests person having surname Ivans has to be at 6:45 & the person at Berkeley must be at 7:15.

7] The two guests appeared in the 6:45 and 7:15 segments can't be Novak, from Daly City or Palo Alto, or interested in bungee jumping (Hint 6). Therefore, these guests must be Cathy and Damien.

8] So for (9) to be Brandon must be at 7:30,  the chef must be at 7:45, and the guest from Sausalito at 8:00.

9] There are 6 different guest pointed by Hint (6). So, the bungee jumper who has to at 7:30 can't be from Daly City or Palo Alto. Hence, he must be from Corte Madera. 

10] Now, Alice has to be from Daly City or Palo Alto & hence can't have surname Novak as (6) points 6 different guests. Therefore, Novak must be at 8:00 and Alice at 7:00 must be Lautremont.

 11] With that, the hint (2) suggests that Damien must be at 6:45 and hence Cathy at 7:15.

12] Now it's clear that, Cathy is from Berkeley & hence as (5) suggests Alice can't be from Dale City and is therefore from Palo Alto. So Krieger must be from Dale City.

13] In the last, as per (5) itself, Kreiger, who is from Daly City, cannot be Francine, and must be named Evan. This leaves Francine at 8:00. 

 

The Unfair Arrangement!

Andy and Bill are traveling when they meet Carl. Andy has 5 loaves of bread and Bill has 3; Carl has none and asks to share theirs, promising to pay them 8 gold pieces when they reach the next town.

They agree and divide the bread equally among them. When they reach the next town, Carl offers 5 gold pieces to Andy and 3 to Bill.

“Excuse me,” says Andy. “That’s not equitable.” He proposes another arrangement, which, on consideration, Bill and Carl agree is correct and fair.

How do they divide the 8 gold pieces?

This is fair arrangement of gold distribution! 

Source 

Correcting The Unfair Arrangement!

How unfair the arrangement was?

First we need to know how 8 loaves (5 of Andy & 3 of Bill) are equally distributes among 3.

If each of them is cut into 2 parts then total 16 loaves would be there which can't be divided equally among 3.

Suppose, each of loaves is divided into 3 parts making total 24 loaves available.

Now, Andy makes 15 pieces of his 5 loaves. He eats 8 and gives the remaining 7 to Carl.

Bill makes 9 pieces of his 3 loaves. He eats 8 and gives the remaining 1 to Carl.

This way, Carl too gets 8 pieces and 8 breads are distributed equally among 3.

 
Obviously, Carl should pay 7 gold pieces to Andy for his 7 pieces and 1 gold piece to Bill for the only piece offered by Bill. 
 

A Check Post At Each Mile

A poor villager grows mango in his land and sells them in the town. The town is 1000 miles away from the village. He has rented a truck for transporting the mangoes to the town. The truck can carry 1000 mangoes at one time and this season, he was able to yield 3000 mangoes.

There is a problem. At each mile till the town, there is a check post at which he must give one mango each while traveling towards the town. However, if he is traveling from the town towards his village, he won’t have to give anything.

Transportation Truck

Tell a way in which the villager can take highest possible number of mangoes to the town.

Know here that highest possible number!

Source 

Smart Saving At Check Posts

How much each check post charging?

Obviously, he can't make 3 trips from town to village straightaway as in that case he wouldn't have anything left (3 x 1000 mangoes paid).

So he need to divide the journey into parts. While breaking journey into parts he has to make sure that after each part he will need less trips to complete the next part.

Now if somehow he pays 1000 mangoes in first part of the journey then for next part he has to make only 2 trips to carry 2000 mangoes.

Part 1 : Hence, he should first make 3 trips till 333 miles. In this part, he would pay 3 x 333 = 999 mangoes leaving 3000 - 999 = 2001 mangoes in stock.

Part : 1

Part 2 : He should leave 1 mango here & take 2000 mangoes further. For next part, he need to make at least 2 trips for 2000 mangoes. In order to save number of trips in next part some how he need to make mangoes in stock less than 1000. For that he should make 2 trips 500 mile further. So he will pay 2 x 500 = 1000 mangoes but having 2000 - 1000 = 1000 mangoes in stock. Still he has to travel 1000 - 500 - 337 = 167 miles.

Part : 2

Part 3 : For next 167 miles, he need to make only 1 trip of 1000 mangoes where he will pay 167 mangoes leaving 1000 - 167 = 833 mangoes. 

Part : 3

This is how he can save 833 mangoes in entire journey. 

Magical Water Well & Pilgrim

In a small town, there are three temples in a row and a well in front of each temple. A pilgrim came to the town with certain number of flowers.

Before entering the first temple, he washed all the flowers he had with the water of well. To his surprise, flowers doubled. He offered few flowers to the God in the first temple and moved to the second temple. Here also, before entering the temple he washed the remaining flowers with the water of well. And again his flowers doubled. He offered few flowers to the God in second temple and moved to the third temple. Here also, his flowers doubled after washing them with water. He offered few flowers to the God in third temple.

There were no flowers left when pilgrim came out of third temple and he offered same number of flowers to the God in all three temples. What is the minimum number of flowers the pilgrim had initially? How many flower did he offer to each God?

Click here to know answers! 

Source 

Flowers Owned By Pilgrim

What are the questions? 

Let's assume that the pilgrim had X number of flowers initially. Suppose that he offered Y flowers to the each God. 

Before entering into the first temple, magical well doubled the flowers he had initially. That means he had 2X flowers before entering into first temple. After offering Y flowers, he had 2X - Y flowers.

Again after visiting first temple he washed flowers in magical well where number of flowers gets doubled. Now, he had 4X - 2Y.

Out of these 4X - 2Y, he offered Y flowers to God in second temple. So he had 4X - 2Y - Y = 4X - 3Y flowers after visiting second temple.

These 4X - 3Y doubled to 8X - 6Y after washing in magical water well. 

At third temple, he offered all the flowers he had which in turn equal to Y as we assumed.

8X - 6Y = Y

8X = 7Y

X/Y = 7/8

This is the ratio of the flowers that pilgrim had to the flowers he offered to each God.

In general, the pilgrim had 7N flowers initially and he offered 8N flowers to each God, where N = 1, 2, 3, 4,

Let's cross verify same with N = 1, meaning that the pilgrim had 7 flowers initially & offered 8 flowers to each God.

Before entering into first temple, the flowers doubled to 14. Out of which, 8 offered at first temple & left 6.

Again 6 doubled to 12 at magical well & 8 out of 12 offered to God at second temple leaving behind 4.

Those 4 again doubled to 8 by magical well & all 8 offered to God at third temple.