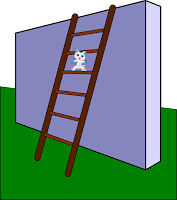
A Determined Cat on a Ladder!

A ladder is leaning against a wall. On the center rung is a cat. She must be a very determined cat, because she remains on that rung as we draw the foot of the ladder away from the tree until the ladder is lying flat on the ground. What path does the cat describe as she undergoes this indignity?

She follows this path!

A Path Followed by Determined Cat

What was the question?

 Interestingly, the cat follows the circular path whose center is at the foot of tree. 

Actually, as ladder is drawn out a series of right triangles with the same hypotenuse (the ladder) are created with respect to the foot of tree.

The point of hypotenuses where cat is sitting determinedly will be always at the same distance from all 3 vertices. So if all such point are joined then we get a circular path having center at the foot of tree. 

(Figure is for illustration purpose only & may not have accurate measurements.

The Mistimed Clock!

Andrea’s only timepiece is a clock that’s fixed to the wall. One day she forgets to wind it and it stops.

She travels across town to have dinner with a friend whose own clock is always correct. When she returns home, she makes a simple calculation and sets her own clock accurately.

 
How does she manage this without knowing the travel time between her house and her friend’s?


That's how she manages to set it accurately!
 

Correcting The Mistimed Clock!

 How it was mistimed?

Andrea winds her clock & sets it to the arbitrary time. Then, she leaves her house and when she reaches her friend's house, she note down the correct time accurately. Now, after having dinner, she notes down the correct time once again before leaving her friend's house.

After returning to home, she finds her own clock acted as 'timer' for her entire trip. It has counted time that she needed to reach her friend's house + time that she spent at her friend's house + time she needed to return back to home.

Since, Andrea had noted timings at which she reached & left her friend's house, she can calculate the time she spent at her friend's house. After subtracting this time duration from her unique timer count she gets the time she needed to reach to & return from her friend's house.

She must have taken the same time to travel from her home to her friend's home and her friend's home to her home. So dividing the count after subtracting 'stay time' she can get how much time she needed to return back to home.

Since, she had noted correct time when she left her friend's home, now by adding time that she needed to return back to home to that, she sets her own clock accurately with correct time.

Let's try to understand it with example.

Suppose she sets her own clock at 12:00 o' clock and leave her house. Suppose she reaches her friend's home and note down the correct time as 3:00 PM. After having dinner she leaves friend's home at 4:00 PM.

After returning back to home she finds her own clock showing say 2:00 PM. That means, she spent 120 minutes outside her home with includes time of travel to and from friends home along with time for which she spent with her friend. If time of stay at her friend is subtracted from above count, then it's clear that she needed 60 minutes to travel to & return back from friend's home.

That is, she needed 30 minutes for travel the distance between 2 homes. Since, she had noted correct time as 3:00 PM when she left friend's home, she can set her own clock accurately at 3:30 PM.

Snail Up The Wall

A snail creeps 10 feet up a wall during the daytime, then falls asleep. It wakes up the next morning and discovers it slipped down 6 feet. If this happens each day, how many days will it take to reach the top of a 20 feet wall?

Escape to answer! 

Source 

A Snail On Top of The Wall !

Read the question first! 

Let's find out progress of snail day by day.

Day 1 : UP to 10, DOWN to 4

Day 2 : UP to 14, DOWN to 8

Day 3 : UP to 18, DOWN to 12

Day 4 : UP to 22 which is greater than 20.

So snail requires 4 days to reach the top of the wall.