Puzzle : The Fake Coin Challenge!

There are 101 coins out of which 1 is fake, the fake coin is identical to a genuine coin but differs in weight. Using weight balance only twice how can we determine whether the fake coin is heavier or lighter than a genuine coin?

 

 

This is how to do it! 

Fake Vs Genuine Coin Weigh Comparison

This was the challenge!

Remember we are asked to determine whether the fake coin is lighter or heavier when compared with the genuine coin and not to identify the fake coin itself.

Keep aside any one coin. Divide remaining 100 coins into 2 groups of 50 coins each. Put these 2 groups on 2 pans of the balance.

1. If they weigh equal the the coin that is kept aside is fake. Weigh it against any genuine among 100 coins to know whether fake coin is lighter or heavier than genuine.

2. If they are not equal then that means the fake coin either made one side heavier or the other side lighter.

3. Take the heavier group of 50 coins for the next test. Divide them into 2 groups of 25 coins each. 

4. Put 25 - 25 coins on weighing balance. If they weigh equal then that means no fake coin among them which also means the fake coin was in the other group of 50 coins which was lighter in the first weighing. 

Hence, the fake coin is lighter present in the other group of 50 coins making the group slightly lighter compared to group of 50 genuine coins.

4.1. And if the result of weighing 25 - 25 coins is unequal then it's clear that the fake coin is among these 50 coins. Also, it must be heavier making this group to weigh more than the other group of 50 genuine coins in the first weighing.

This way, we can determine whether the fake coin is heavier or lighter than genuine one using the weighing balance only twice.

The Watermelon Paradox

There is a 100 pound watermelon laying out in the sun. 99 percent of the watermelon's weight is water. After laying out for a few hours 98 percent of the watermelon's weight is water.

How much water evaporated?

The calculation is TRICKY one! 

Tricky Watermelon Water Weight Calculation

What is the question?

Initially, since 99% of watermelon is water, the weight of water must be 99 pounds and weight of other stuffs should be 1 pound.

After evaporation, 98% of watermelon is water indicates that the there is 2% of other stuff present at the point of time. 

That is, if we assume the weight of other stuff unchanged during evaporation, now 1 pound itself is equal to the 2% of total weight of watermelon.

In other words, the process of evaporation increased percent weight of other stuffs in total weight of watermelon from 1% to 2%.

If W is the total weight of watermelon, then weight of other stuffs (which is 1 pound)

W x (2/100) = 1 pound

W = 50 Pounds.

Out of these 50 pound, 1 pound (2% of total weight) is other stuffs and 49 pounds is water (98% of total weight).

That means, out of 99 pounds of water, 99 - 49 = 50 pounds of water is evaporated in the process. 

Heavier Vs Lighter Balls

We have two white, two red and two blue balls. For each color, one ball is heavy and the other is light. All heavy balls weigh the same. All light balls weigh the same. How many weighing on a beam balance are necessary to identify the three heavy balls? 

You need only 2 weighings! Click here to know how!

Identifying The Heavier/Lighter Balls

What was the task given?

Actually, we need only 2 weighing. 

Weigh 1 red & 1 white ball against 1 blue & 1 white ball. Weighing result between these balls helps us to deduce the relative weights of other balls.
  ----------------------------------------------------------------------------------------------------

Case 1 : 

If this weighing is equal then the weight of red ball and blue ball are different.
That's because the weighing is equal only when there is combination of 
H (Heavy) + L (Light) against L (Light) + H (Heavy). 

Since, one white ball must be heavier than the other white ball placed in other pan, the red & blue balls place along with them must be of 'opposite' weights with respect to the white balls place along with them.

So weigh this red against blue will give us the heavier red (or blue) leaving other red (or blue) as lighter. 

If red (or blue) weighs more in this weighing then the white ball placed with this red (or blue) in first weighing must be lighter than the other white ball placed with blue (or red) ball.  

----------------------------------------------------------------------------------------------------

Case 2 : Red + White > Blue + White.

The white ball in Red + White must be heavier than the white ball in Blue + White.

The reason is if this white was lighter then even heavier red in the Red + White can't weigh more than Blue + White having heavier white. That is H + L can't beat H + H or obviously would equal with H + L!

So we have got the heavier and lighter white balls for sure.

Now, weigh red from Red + White and blue from Blue + White against other red and blue balls left.

     Case 2.1/2.2 : Red + Blue > or < Red + Blue 

     Obviously, red and blue balls in left pan are heavier (or lighter) than those in other.
    
     ------------------------------------------------------------------------------------

     Case 2.3 :  Red + Blue = Red + Blue 

     Obviously, that's because of H + L = L + H.

      But the red is taken from Red + White which was heavier than the Blue + White. 
      Since, L + H (white is heavier as concluded) can't weigh more than H + L
      (other white is lighter as concluded) or L + L, the red in Red + White 
      must be heavier making H + H combination in that pan in first weighing (case 2). 

      So, we got heavier red and lighter blue obviously leaving lighter red 
      and heavier blue in other pan. 

----------------------------------------------------------------------------------------------------

Case 3 : Red + White < Blue + White.

Just replace Red with blue & vice versa in the deduction made in case 2. 

----------------------------------------------------------------------------------------------------

"Are you holding true or fake coin?"

You have 101 coins, and you know that 50 of them are counterfeit. Every true coin has the same weight, an unknown integer, and every false coin has the same weight,which differs from that of a true coin by 1 gram. You also have a two-pan pointer scale that will show you the difference in weight between the contents of each pan. You choose one coin. 

Can you tell in a single weighing whether it’s true or false?

Well, this trick will help you to identify that coin! 

Knowing The Truth of the Coin in Hand!

What was the task given?

Yes, you can tell that whether the coin is true or false with single weighting.Just divide 100 coins into 2 groups of 50 coins each & put into 2 pans of weighing balance.

Let's assume true coin weighs 1 gram (or 2 gram) & fake coin weighs 2 gram (or 1 gram). Remember, if the sum of 2 integers is even then difference between two is bound to be even. And if the sum of those is odd then difference between them has to be odd.

CASE 1 :

If the coin that you are holding is true then the total weight on the balance will be
50 + (50x2) = 50 + 100 = 150  (or 50x2 + 50 = 150). So, the total sum of weights in 2 pans is even, hence difference between them has to be even. For example, if those 150 grams are distributed as 80 vs 70 then difference between them is 10 which is even.


CASE 2 :

If the coin you are holding is fake then the total weight on the balance will be
51 + (49x2) = 51 + 98 = 149 (or 51x2 + 49x1 = 153).

Here, total is odd hence the difference must be odd too. For example, if above 149 grams are distributed as 90 vs 59 then pointer of balance will point at 31 which is odd.

Conclusion:

In short, you have to notice the difference between 2 weights on the pans. If it's even then the coin you are holding is true and if difference is odd then you are holding a fake coin.
 

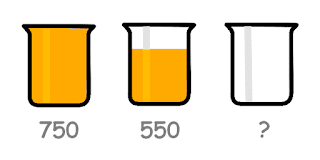
What is the Weight of the Empty Jar?

A full jar of honey weighs 750 grams, and the same jar two-thirds full weighs 550 grams.

What is the weight of the empty jar in grams?

Find the correct way to find the weight here!

Calculation of Weight of the Empty Jar

Collect the given data.

Let J be the weight of empty jar and H be the weight of honey when jar was full.

J + H = 750                                            ......(1)

And in second case,

J + (2/3)H = 550                                     .....(2) 

Subtracting (2) from (1),

(1/3)H = 200

Hence, H = 600.

Putting this value in (1),

J = 750 - 600 = 150.

Therefore, the weight of the empty jar is 150 grams.

How it Will Affect the Water Level?

A man stuck in a small sailboat on a perfectly calm lake throws a stone overboard. It sinks to the bottom of the lake.

When the water again settles to a perfect calm, is the water level in the lake higher, lower, or in the same place compared to where it was before the stone was cast in?

Did you think it will rise? 

Physics : Finding the Effect on the Water Level

But why water level was affected?

Do you recall what does Archimedes Principle state? For an object to float on water, it has to displace that much volume of water whose weight is equal to weight of the object itself. Now if object has less density than water then obviously it has to displace lesser amount of volume of water to float on it. That means it has to sink less in water.

For a moment, let's assume the stone has very high density & hence having weight equal to hundreds of kilograms despite of having small volume.

Here, stone sinks to the bottom of the lake suggests that it is has more density than water. It can't displace the water whose weight is equal to it's weight.But when it was on sailboat it could push the sailboat down so that more water is displaced weighing equal to it's weight. Result of this, the sailboat sinks little 'deeper' compared to when stone wasn't there.

Obviously, the volume of displaced water when stone was in sailboat (due to stone only) must be greater that the volume of displaced water when stone sinks to the bottom of the lake. That's why both sailboat and stone together could float on the water. In short, sailboat helped stone to displace amount of water needed to float which results in rise in shoreline.

And when stone is thrown out of the sailboat, then ideally it can't displace more water than when it was on sailboat. Now, sailboat sinks less 'deeper' in water displacing only water need to float itself. 

That's why the water level must be dropped compared to earlier. The little rise due to water displaced by stone can't exceed the earlier water level for the reason explained above.