Skip to main content
Posts
A team of three people decide on a strategy for playing the following
game.
Each player walks into a room. On the way in, a fair coin is
tossed for each player, deciding that player’s hat color, either red or
blue. Each player can see the hat colors of the other two players, but
cannot see her own hat color.
After inspecting each other’s hat colors,
each player decides on a response, one of: “I have a red hat”, “I had a
blue hat”, or “I pass”. The responses are recorded, but the responses
are not shared until every player has recorded her response.
The team wins
if at least one player responds with a color and every color response
correctly describes the hat color of the player making the response. In
other words, the team loses if either everyone responds with “I pass” or someone responds with a color that is different from her hat color.
What strategy should one use to maximize the team’s expected chance of winning?
These could be the strategies to maximize the chances of winning!
What's the puzzle?
There can be two strategies to maximize the chances of winning in the game.
STRATEGY - 1 :
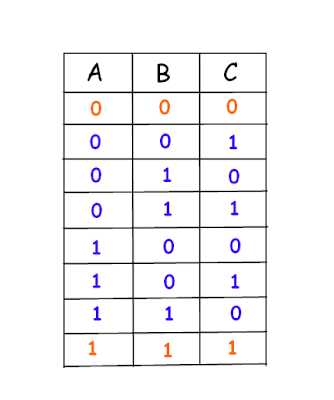
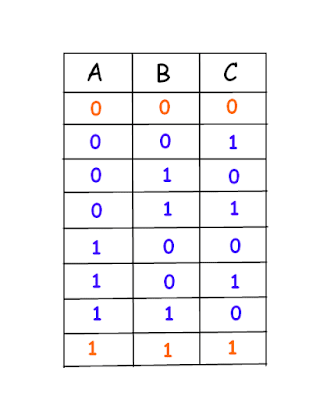
There are 8 different possible combinations of three color hats on the heads of 3 people. If we assume red is represented by 0 & blue by 1 then those 8 combinations are -
Here only 2 combinations are there where all are wearing either red or blue hats. That is 2/8 = 25% combinations where all are wearing hat of same color and 6/8 = 75% combinations where either 1 is wearing the different colored hat than the other 2. In short, at least 2 will be wearing either red or blue in 75% of combinations.
Now for any possible combination, there will be 2 hats of the same color (either blue or red). The one who sees the same color of hats on heads of other two should tell the opposite color as there are 75% such combinations. That will certainly increase the chances of winning to 75%.
STRATEGY 2 :
Interestingly, here 3 responses from each member of team are possible viz RED (R), BLUE (B) and PASS (P). And every member can see 3 possible combinations of hats on the heads of other 2 which are as 2 RED (2R), 2 BLUE (2B) and 1RED:1BLUE (RB). See below.
Let's think as instructor of this team. We need to cover up all the possible 8 combinations in form of responses in the above table.
For every possible combination, at least 1 response need to be correct to ensure win. But out of 9 above, 3 responses of 'PASS' are eliminated as they won't be counted as correct responses. So we are left with only 6. Let's see how we can do it.
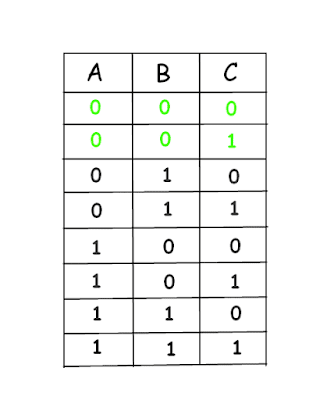
First of let's take case of 2R. There are 2 responses where A sees 2 RED hats (000,100). We can't make sure A's response correct in both cases. So let A's response for this case be R. So whenever this 000 combination will appear A's response will secure win.
After covering up 000, let's cover up 001. For that, C's response should be B whenever she sees 2 red hats on other 2. And only left response P would be assigned to B.
So far,we have covered up these 2 combination via above responses.
--------------------------------------------------------------------------
Now, let's take a case of 2B. A can see 2B hats whenever there 011 or 111 appears. Since A's R response is already used previously, let B be her response in the case. So the combination 111 will be covered up with A's response.
B can see 2B hats in case of 101 or 111. Since 111 is already covered above, to cover up 101, B should say R whenever she sees 2 BLUE hats on the heads of other 2. With this only response left for C in case of 2B is P.
With these responses, we have covers of so far,
-------------------------------------------------------------------------
After filling remaining 1 possible response in response table for every team member in case of 1 RED and 1 BLUE hat,
B's response as BLUE in this case will ensure win whenever 011 or 110 combination will appear. Similarly, C's response as a RED will secure win whenever 010 or 100 appears as a combination.
------------------------------------------------------------------------------
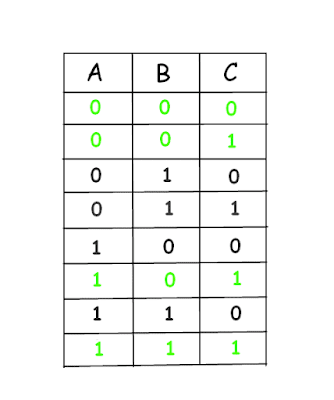
In this way, there will be at least 1 response correct for every possible 8 combinations. This strategy will give us 100% chances of winning this game!
The above table shows who is going to respond correctly for the given combination ( the block of combination & correct response are painted with the same background color).
SIMPLE LOGIC :
The same strategy can be summarized with very simple logic.
There must be someone to say RED whenever she sees 2 RED hats; someone should say BLUE and remaining one should say PASS. Similarly, one has to say BLUE; other should say RED & third one should say PASS whenever 2 BLUE hats are seen. Same logic to be followed in case of 1 RED and 1 BLUE hats seen. But while doing this, we need to make sure responses are well distributed & not repeated by single member of team (See table below).