Skip to main content
Posts
There is a building of 100 floors.
-If an egg drops from the Nth floor or above it will break.
-If it’s dropped from any floor below, it will not break.
You’re given 2 eggs.
Find N.
How many drops you need to make?
What strategy should you adopt to minimize the number egg drops it takes to find the solution?
'This' should be the strategy!
What was the task?
Let's suppose, the we drop the egg from N the floor & it breaks then we need to do linear search till (N-1) th floor. For example, we dropped egg from 10 the floor & it breaks then we need to test 1-9 floors using 2nd egg to find the exact floor from which the egg breaks on dropping. So the best case would be 10 drops if the first egg breaks when dropped from 10 the floor.But that's only possible if the egg breaks on drop from 10th floor.
The worst case would be when egg doesn't break at 10,20,30,40,50,60,70,80,90 and breaks at 100th floor. Here, once again 91-99 need to be tested using other egg to find exact floor from which egg will break on drop.So in worst case, 19 drops would be needed.
Best way to minimize the number of drops required is to minimize the linear search (91-99 above in worst case) that we need to do with the second egg after 1st egg breaks on drop from particular floor (100th floor in above worst case).
So after dropping egg from N th floor & if egg doesn't break then instead of going to next Nth floor, better to go N + (N-1) th floor. And now if the egg break here at N + (N-1) th floor then we need to do linear search from (N+1) th floor to N + (N-1) th floor instead of (N+1) th floor to (N + N) th floor. That's 1 less linear search than that needed if we go to the next N th floor if egg doesn't break on drop from Nth floor.
After dropping egg from N + (N-1) th floor, if it doesn't break then we should go the the N + (N-1) + (N-2) th floor.
Adding all instances of drops i.e. drop at Nth, drop at N + (N-1) th , drop at N + (N-1) + (N-2) & so on gives us
N + (N-1) + (N-2) + (N-3).......+1 = N(N+1)/2.
which shouldn't exceed 100 as there are only 100 floors & hence total number of drops must not be greater than 100.
So,
N(N+1)/2 >= 100
N^2 + N - 200 >= 0
This is
This is quadratic equation in form ax^2 + bx + c = 0 where x = [-b +- (b^2 -4ac)^0.5]/2a.
Solving above for N gives,
N = 13.651
Rounding value of N to 14 in the case.
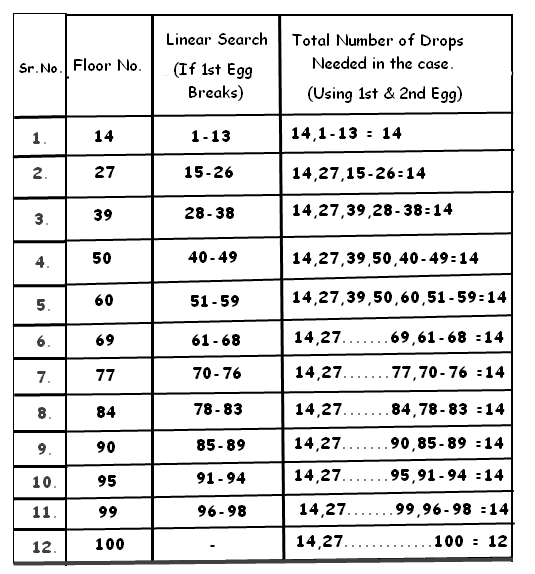
So we should start with floor no. 14 followed by 27,39,50,60,69,77,84,90,95,99,100
In the worst case here total drops needed are only 14.
For example, if the egg breaks when dropped from 14th floor then for second egg we need to test 1-13 floors to find the exact floor from which egg breaks on the drop. See table below.
Similarly, for example, egg breaks after drop from 50 floor (after testing 14,27,39), we need to test at 51-59 floors by dropping second egg to know the exact floor from where egg breaks on the drop.