Skip to main content
Posts
A
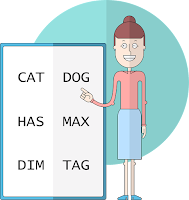
teacher writes six words on a board: “cat dog has max dim tag.” She
gives three students, Albert, Bernard and Cheryl each a piece of paper
with one letter from one of the words.
Then she asks, “Albert, do you
know the word?” Albert immediately replies yes.
She asks, “Bernard, do
you know the word?” He thinks for a moment and replies yes.
Then she
asks Cheryl the same question. She thinks and then replies yes.
What is
the word?
THIS must be the given word!
What was the puzzle?
A teacher writes six words on a board: CAT, DOG, HAS, MAX, DIM, TAG
--------------------------------------------------------------------------------------------------
1. Albert knows the word right away because he must have received unique letter from above words. Had he received the letter A then he wouldn't have figured out the exact word as A appears in CAT, HAS, MAX and TAG.
Similarly, he must not have received letters T, D, M and G as those appears multiple times in the list of words.
That is, he must have letter from unique letters C, O, H, S, X, I as they appears only once in the above list of words.
With that the word TAG is eliminated out of the race since any of unique letters doesn't appear in the word TAG.
--------------------------------------------------------------------------------------------------
2. Now, words left are - CAT, DOG, HAS, MAX, DIM
In a moment of thinking, Bernard can conclude that the TAG can't be the word and Albert must have got some unique letter from the given words.
After providing letter from C, O, H, S, X, I to Albert, teacher provides letter from rest of letters to Bernard.
Now, if she had given letter -
A - Bernard wouldn't have idea whether the word is CAT, HAS or MAX
D - Bernard wouldn't have idea whether the word is DOG or DIM
M - Bernard wouldn't have idea whether the word is MAX or DIM
That is she must had given letter from unique letters T, O, G, H, S, X.
So, at start, if she provides letter I to the Albert then she can't provide D or M of word DIM to Bernard to give him equal chance to identify the word.
Hence, the word DIM is also eliminated out of race.
If she had provided letter O to Bernard, then Albert would have been with either D or G with which he wouldn't have been able to figure out the exact word whether it is DOG/DIM or DOG/TAG respectively. Hence, Bernard must not be with letter O.
If Bernard is with letter X then Albert must had either M or A with which he couldn't have figured out the exact word among MAX/DIM or CAT/HAS/TAG/MAX. Hence, Bernard can't have X as well. With that MAX is also eliminated.
Now, if Bernard has letter -
T - Albert might be with C
G - Albert might be with O
H - Albert may have S
S - Albert may have H.
--------------------------------------------------------------------------------------------------
3. The words left are - CAT, DOG, HAS.
Again, in a moment of thinking, Cheryl deduced list of 3 possible words as above.
Now, if she had letter A then she wouldn't have idea of exact word whether it is CAT or HAS.
If she had unique letter among C/T (or H/S), then either Albert or Bernard with letter A would have been unsuccessful in guess.
If she had letter O/G then either Albert of Bernard would have been with letter D by which they wouldn't know the exact word.
Hence, Cheryl must had letter D and the word must be DOG.
Albert must have got letter O and the Bernard must have received letter G.
--------------------------------------------------------------------------------------------------