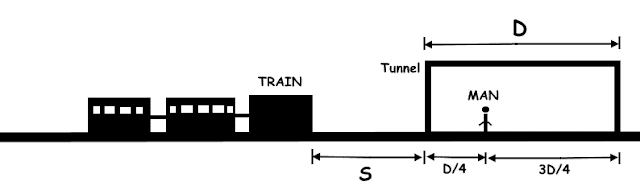
The Tunnel Trouble!

A man needs to go through a train tunnel to reach the other side. He starts running through the tunnel in an effort to reach his destination as soon as possible. When he is 1/4th of the way through the tunnel, he hears the train whistle behind him. 

Assuming the tunnel is not big enough for him and the train, he has to get out of the tunnel in order to survive. We know that the following conditions are true - 

1. If he runs back, he will make it out of the tunnel by a whisker.

2. If he continues running forward, he will still make it out through the other end by a whisker.

What is the speed of the train compared to that of the man?

The train must be traveling at THIS speed!

Escape From The Tunnel Trouble!

What was the question?

LOGICAL APPROACH : 

As per condition, if the man runs back he will make it out of the tunnel by a whisker. That means while he runs back 1/4 th tunnel distance, the train travels from it's position to the start of the tunnel. 

In other words, the time taken by man to get back covering 1/4th to the start of the tunnel and the time taken by train to reach at the start of tunnel is same.

So if the man decides to go forward then by time the train reaches at the start of tunnel, man covers another 1/4th tunnel distance i.e. he will be halfway of the tunnel.

At this point of time, the man needs to cover another 1/2th tunnel distance while train has to cover entire tunnel distance. Since, man just manages to escape from accident with train at the exit of tunnel, the train speed has to be double than man's speed as it has to travel distance double of that man travels.

MATHEMATICAL APPROACH : 

Let us suppose - 

M - Speed of Man

T - Speed of Train

D - Tunnel Distance/length

S - Distance between train and the start of tunnel.

As per condition 1, 

Time needed for man to get back at the start of tunnel = Time needed for train to cover distance F to arrive at the start of tunnel

(D/4)/M = S/T  

D/4M =  S/T  .....(1)

As per condition 2,

Time needed for man to move forward at the end of tunnel = Time needed for train to cover distance S + time needed to cover tunnel distance.

(3D/4)/M = S/T + D/T 

Putting S/T = D/4M,

3D/4M - D/4M = D/T

2D/4M = D/T

T/M = 2

T = 2M.

That is speed of the train needs to be double of the speed of the man.

Interestingly, from (1),

D/S = 4M/T

D/S = 2 

D = 2S

S = D/2

That is train is 1/2th tunnel distance away from the start of tunnel.