Skip to main content
Posts
A dead body lies at the bottom of a multistory building. It looks as though he committed suicide by jumping from one of the floors.
When the detective arrives, he goes to the first floor of the building, opens the closed window, and flips a coin towards the floor. He goes to the second floor and does the exact same thing. He continues to do this until he gets to the top floor of the building.
When he comes back down, he states that it was a murder and not a suicide. How does he know that?
(Entry to the terrace was banned due to some ongoing work).
Read the detective's logic in the case!
What is the case?
Obviously, the person can't jump with window closed or come outside of the window & close that window from inside.
The detective checks if windows is closed from inside by opening window & flipping the coin toward the floor. He flips the coin to mark the count of that particular floor where window was closed from inside & he has to open it to flip the coin.
At the end, he collects as many coin as floors of that building. So he concludes that no floor had open window from where the person might have jumped.
So, he concludes that it was the murder and not the suicide.
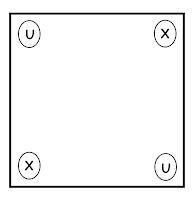
Four glasses are placed on the corners of a square table. Some of the
glasses are upright (up) and some upside-down (down). A blindfolded
person is seated next to the table and is required to re-arrange the
glasses so that they are all up or all down, either arrangement being
acceptable, which will be signaled by the ringing of a bell.
The
glasses may be re-arranged in turns subject to the following rules.
1.Any
two glasses may be inspected in one turn and after feeling their
orientation the person may reverse the orientation of either, neither or
both glasses.
2.After each turn the table is rotated through a random
angle.
3.The puzzle is to devise an algorithm which allows the blindfolded
person to ensure that all glasses have the same orientation (either up
or down) in a finite number of turns. The algorithm must be
non-stochastic i.e. it must not depend on luck.
Here is that algorithm!
What was the puzzle?
Below is the algorithm which makes sure the bell will ring in at most five turns.
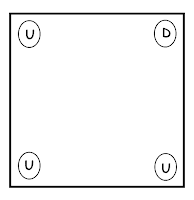
1.On the first turn choose a diagonally opposite pair of glasses and turn both glasses up.
At this point, the position of other 2 glasses is not known.
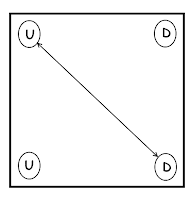
2.On the second turn, choose 2 adjacent glasses. One of them was turned up in the previous step, so other may or may not in up position. If the other is down then turn it up and if remaining one X is also in up position then bell will be rung.
If the bell does not ring then there are now three glasses up and one down(3U and 1D).
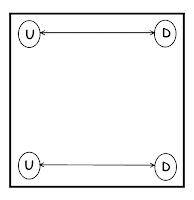
3.On the third turn choose a diagonally opposite pair of glasses. If one is down, turn it up and the bell will ring.
And if you find both are up, then you must have chosen other diagonally opposite pair.
If so, then turn one down so that 2 glasses are up and other 2 are down.
4.On the fourth turn choose two adjacent glasses and reverse both. If both were in the same orientation then the bell will ring.
And in case, if you find one is up and other down like -
still reverse orientation of both as -
Now diagonally opposite pairs are either up or down.
5.On the fifth turn choose a diagonally opposite pair of glasses and reverse both.
The bell will ring for sure.
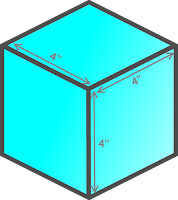
A solid, four-inch cube of wood is coated with blue paint on all six
sides.
Then the cube is cut into smaller one-inch cubes. These new
one-inch cubes will have either three blue sides, two blue sides, one
blue side, or no blue sides. How many of each will there be?
Here is solution of the puzzle!
What is the puzzle?
Apart from the 8 cubes at the center all 4 x 4 x 4 - 8 = 56 will have some paint on ones side at least. See below the 1/4 th cube is taken out.
The cubes at the 8 corners will have blue paint on three sides.
The cubes between corner cubes along 12 edges of big cube will have 2 sides painted. That is 12 x 2 = 24 cubes will painted with blue on 2 sides.
And 4 center cubes on each of 6 faces (left, right, top, bottom, front, back) will have only 1 side painted with blue. That is , there are 6 x 4 = 24 cubes having paint on one side only.
To conclude, out of 56 painted cubes,
24 cubes have paint on 1 side,
24 cubes painted with 2 sides,
8 are painted with three sides.
This puzzle has been attributed both to Lewis Carroll and to Albert Einstein:
- There are five houses in a row. Each of the houses is painted a
different color, and their occupants come from different countries, own
different pets, drink different beverages, and smoke different cigarette
brands.
- The Englishman lives in the red house.
- The Spaniard owns the dog.
- Coffee is drunk in the green house.
- The Ukrainian drinks tea.
- The green house is immediately to the right (your right) of the ivory house.
- The Old Gold smoker owns snails.
- Kools are smoked in the yellow house.
- Milk is drunk in the middle house.
- The Norwegian lives in the first house.
- The man who smokes Chesterfields lives in the house next to the man with the fox.
- Kools are smoked in the house next to the house where the horse is kept.
- The Lucky Strike smoker drinks orange juice.
- The Japanese smokes Parliaments.
- The Norwegian lives next to the blue house.
Who drinks water? Who owns the zebra?
Well, here is effort to simplify the solution
From Wikipedia : The puzzle is often called Einstein's Puzzle or Einstein's Riddle because it is said to have been invented by Albert Einstein as a boy; it is also sometimes attributed to Lewis Carroll. However, there is no known evidence for Einstein's or Carroll's authorship and the Life International version of the puzzle mentions brands of cigarette, such as Kools, that did not exist during Carroll's lifetime or Einstein's boyhood.