Skip to main content
Posts
What was the task?
Let's suppose, the we drop the egg from N the floor & it breaks then we need to do linear search till (N-1) th floor. For example, we dropped egg from 10 the floor & it breaks then we need to test 1-9 floors using 2nd egg to find the exact floor from which the egg breaks on dropping. So the best case would be 10 drops if the first egg breaks when dropped from 10 the floor.But that's only possible if the egg breaks on drop from 10th floor.
The worst case would be when egg doesn't break at 10,20,30,40,50,60,70,80,90 and breaks at 100th floor. Here, once again 91-99 need to be tested using other egg to find exact floor from which egg will break on drop.So in worst case, 19 drops would be needed.
Best way to minimize the number of drops required is to minimize the linear search (91-99 above in worst case) that we need to do with the second egg after 1st egg breaks on drop from particular floor (100th floor in above worst case).
So after dropping egg from N th floor & if egg doesn't break then instead of going to next Nth floor, better to go N + (N-1) th floor. And now if the egg break here at N + (N-1) th floor then we need to do linear search from (N+1) th floor to N + (N-1) th floor instead of (N+1) th floor to (N + N) th floor. That's 1 less linear search than that needed if we go to the next N th floor if egg doesn't break on drop from Nth floor.
After dropping egg from N + (N-1) th floor, if it doesn't break then we should go the the N + (N-1) + (N-2) th floor.
Adding all instances of drops i.e. drop at Nth, drop at N + (N-1) th , drop at N + (N-1) + (N-2) & so on gives us
N + (N-1) + (N-2) + (N-3).......+1 = N(N+1)/2.
which shouldn't exceed 100 as there are only 100 floors & hence total number of drops must not be greater than 100.
So,
N(N+1)/2 >= 100
N^2 + N - 200 >= 0
This is
This is quadratic equation in form ax^2 + bx + c = 0 where x = [-b +- (b^2 -4ac)^0.5]/2a.
Solving above for N gives,
N = 13.651
Rounding value of N to 14 in the case.
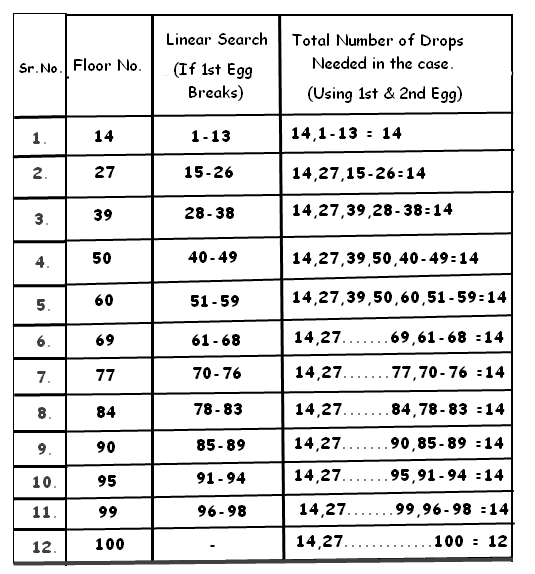
So we should start with floor no. 14 followed by 27,39,50,60,69,77,84,90,95,99,100
In the worst case here total drops needed are only 14.
For example, if the egg breaks when dropped from 14th floor then for second egg we need to test 1-13 floors to find the exact floor from which egg breaks on the drop. See table below.
Similarly, for example, egg breaks after drop from 50 floor (after testing 14,27,39), we need to test at 51-59 floors by dropping second egg to know the exact floor from where egg breaks on the drop.
How boxes are placed?
Let's assume a, b, c and d are the correct numbers in the boxes.
So, 4 equations that we get are,
a + b = 8 .....(1)
c - d = 6 .....(2)
a + c = 13 .....(3)
b + d = 8 .....(4)
Subtracting (1) from (3) gives,
c - b = 5 .....(5)
Adding (2) to (4),
c + b = 14 .....(6)
Adding (5) and (6) gives,
2c = 19
c = 9.5
Putting c = 9.5 in (2),
9.5 - d = 6
Hence, d = 3.5
Putting d =3.5 in (4),
b + 3.5 = 8
b = 4.5
Putting b = 4.5 in (1),
a + 4.5 = 8
a = 3.5
So to conclude, a = 3.5, b = 4.5, c = 9.5 and d = 3.5.
You’re a knight in love with a princess. Unfortunately, the king knows you’re poor and disapproves of the match.
On the night of a great feast, the king calls you up before his men and presents a golden box. In it are two folded slips of paper. One, he announces, reads “Marriage,” the other “Death.” “Choose one,” he says.
Pretending to stir the fire, the princess manages to whisper that both slips say “Death.” But the king and his men are waiting, and you cannot escape now.
What should you do?
This is how you can escape!
What was the biggest challenge in getting that?
All you need to do is take either slip & drop it into the fire.
Now you can say, "Sorry, I couldn't manage to read my fate. But we have option to read what it was. It must be the opposite of what other slip reads.".
And obviously, other slip has 'Death' is written so no one can object that one that dropped in fire must had 'Marriage'. Any claim saying other too had 'Death' would raise the question of credibility of the king directly; so no one would dare to claim that.
Two women are selling apples. The first sells 30 apples at 2 for $1,
earning $15. The second sells 30 apples at 3 for $1, earning $10. So
between them they’ve sold 60 apples for $25.
The next day they set the same goal but work together. They sell 60
apples at 5 for $2, but they’re puzzled to find that they’ve made only
$24.
What became of the other dollar?
Here, could be that lost dollar!
What is the conundrum?
They sell 60 apples at 5 for $2, that means 12 such sets of 5 apples. Suppose, out of each such set, 1 woman takes out $1 for 2 apples and other takes $1 for 3 apples. So, first woman earns $12 by selling 24 apples and second woman sells 36 apples for $12.
In short, first woman gives away 6 apples (from her 30 apples) to second woman increasing her count to 36 reducing her own count to 24. First woman would have made $3 from those but second woman only made $2 from those 6 apples. And there is that lost dollar in earning.
So, 60 apples can't be divided equally to find the earning as they had sold apples at different rates on previous day.
Other way, if they wanted to sell apples together with 30 apples each, then they should have sold apples at average of (1/2 + 1/3)/2 = $5/12 per apple (i.e. 12 apples for $5) instead of $2/5 per apple.
The difference in price per apple (5/12 - 2/5) = (1/60).
So the difference in earning after selling 60 such apples = (1/60) x 60 = 1.
And there is that other dollar!
What's wrong gone here on next day? Instead of averaging dollars per apple, apples per dollar are added directly which resulted reduced cost of each apple.