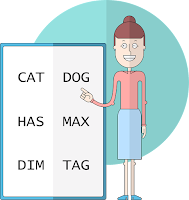
The Secret Word - Puzzle

A teacher writes six words on a board: “cat dog has max dim tag.” She gives three students, Albert, Bernard and Cheryl each a piece of paper with one letter from one of the words.

Then she asks, “Albert, do you know the word?” Albert immediately replies yes.

She asks, “Bernard, do you know the word?” He thinks for a moment and replies yes. 

Then she asks Cheryl the same question. She thinks and then replies yes. 

What is the word?

THIS must be the given word! 

The Secret Word - Solution

What was the puzzle?

A teacher writes six words on a board: CAT, DOG, HAS, MAX, DIM, TAG 

--------------------------------------------------------------------------------------------------

1. Albert knows the word right away because he must have received unique letter from above words. Had he received the letter A then he wouldn't have figured out the exact word as A appears in CAT, HAS, MAX and TAG. 

Similarly, he must not have received letters T, D, M and G as those appears multiple times in the list of words.


That is, he must have letter from unique letters C, O, H, S, X, I as they appears only once in the above list of words.

With that the word TAG is eliminated out of the race since any of unique letters doesn't appear in the word TAG.

--------------------------------------------------------------------------------------------------

2. Now, words left are - CAT, DOG, HAS, MAX, DIM 

In a moment of thinking, Bernard can conclude that the TAG can't be the word and Albert must have got some unique letter from the given words.

After providing letter from C, O, H, S, X, I to Albert, teacher provides letter from rest of letters to Bernard.


Now, if she had given letter -

A - Bernard wouldn't have idea whether the word is CAT, HAS or MAX

D - Bernard wouldn't have idea whether the word is DOG or DIM

M - Bernard wouldn't have idea whether the word is MAX or DIM

That is she must had given letter from unique letters T, O, G, H, S, X.

So, at start, if she provides letter I to the Albert then she can't provide D or M of word DIM to Bernard to give him equal chance to identify the word. 

Hence, the word DIM is also eliminated out of race.

If she had provided letter O to Bernard, then Albert would have been with either D or G with which he wouldn't have been able to figure out the exact word whether it is DOG/DIM or DOG/TAG respectively. Hence, Bernard must not be with letter O.

If Bernard is with letter X then Albert must had either M or A with which he couldn't have figured out the exact word among MAX/DIM or CAT/HAS/TAG/MAX. Hence, Bernard can't have X as well. With that MAX is also eliminated.

Now, if Bernard has letter - 

T - Albert might be with C

G - Albert might be with O

H - Albert may have S

S - Albert may have H. 

--------------------------------------------------------------------------------------------------

3. The words left are - CAT, DOG, HAS.

Again, in a moment of thinking, Cheryl deduced list of 3 possible words as above.

Now, if she had letter A then she wouldn't have idea of exact word whether it is CAT or HAS. 


If she had unique letter among C/T (or H/S), then either Albert or Bernard with letter A would have been unsuccessful in guess.

If she had letter O/G then either Albert of Bernard would have been with letter D by which they wouldn't know the exact word. 

Hence, Cheryl must had letter D and the word must be DOG.

Albert must have got letter O and the Bernard must have received letter G.

--------------------------------------------------------------------------------------------------

"What day is it?"

A girl meets a lion and unicorn in the forest. The lion lies every Monday, Tuesday and Wednesday and the other days he speaks the truth. The unicorn lies on Thursdays, Fridays and Saturdays, and the other days of the week he speaks the truth. 

“Yesterday I was lying,” the lion told the girl. “So was I,” said the unicorn. 

What day is it?

It must be .... day of the week. Click to know.

"The day must be a Thursday!"

Little story behind the title! 

Lion lies on Mondays, Tuesdays, and Wednesdays and The Unicorn, on the other hand, lies on Thursdays, Fridays, and Saturdays.


That is on Sundays both must be telling the truth. 

Suppose Lion and Unicorn made those statements today.

Lion - “Yesterday I was lying,”  

Unicorn - “So was I,”  (“Yesterday I was too lying,” ) 

If it was Sunday today, then Lion's statement would have been lie as lion tells truth on Saturdays. But as per data, both must be telling the truth on Sundays. So it can't be Sunday today.

For rest of all days, one must be telling the truth and other must be lying.

---------------------------------------------------------------------------------------------------------------

CASE 1 : Lion is lying and Unicorn is truth teller.

For Unicorn's statement - “Yesterday I too was lying,” to be true it must be Sunday today. But on Sunday, lion also speaks truth. And lion's statement can't be true on Sunday as concluded earlier. 

Hence, today must be the case below.

------------------------------------------------------------------------------------
   
CASE 2 : Lion is truth teller and Unicorn is lying.

Again for Lion's statement - “Yesterday I was lying,” to be true it must be Thursday today. 

And if today is Thursday Unicorn is lying with it's statement - "“Yesterday I too was lying,” as it was Wednesday yesterday where Unicorn always tells truth on Wednesday. 

Hence, today, on Thursday, Unicorn must be lying with his statement while Lion is telling the truth. Both are as per behaving the given data.

 

The Allotment Challenge?

Five bankers are sharing 12 golden ingots. They decide to proceed that way : 

The elder one will suggest an ingots allotment. The rest will vote for or against it. If the majority accepts, the sharing is ratified. If not, the elder will be dismissed. So, the sharing would be done between the remaining banker with the same rules. 

Knowing that they are set from left to right in a diminishing order of their ages, how would be the allotment ?

THIS should be the UNDENIABLE Allotment!

Source 

The Undenial Allotment Proposition!

What were rules of allotment process?

The eldest should allot ingot like 9, 0, 1, 0, 2 among 5 bankers.

Let's name bankers as Banker 5, Banker 4 ...... Banker 1 according to decreasing order of their ages.

------------------------------------------------------------------------------

CASE 1 : 

Suppose there are only 2 bankers left then the youngest will always deny whatever elder offers so that he can take away all 12 ingots on his turn.

------------------------------------------------------------------------------

CASE 2 : 

If case is reduced to 3 bankers then the eldest knows that the youngest is not going to agree with him in any case. With that, the eldest will be dismissed and case reduced to CASE 1 where youngest can take away all. 

So, the eldest here proposes allotment as 11, 1, 0. The Banker 2 has no option than to accept this proposal otherwise he won't get anything if case is reduced to 2 bankers as in CASE 1 above.

------------------------------------------------------------------------------

CASE 3 : 

With 4 bankers, the eldest would propose allotment 9, 0, 2, 1.

In the case, Banker 3 will never accept any proposal as after banker 4 is dismissed he would be getting 11 ingots as in CASE 2 above.

The Banker 2 will happily agree with the eldest as he would be getting 1 more ingot than the CASE 2. 

And Banker 1 knows he will be getting nothing if the case is reduced to 3 bankers as in CASE 2. So, he too will agree with the eldest in the case.

------------------------------------------------------------------------------

CASE 4 : 

With 5 bankers, the eldest i.e. Banker 5 should propose allotment 9,0,1,0,2.

Obviously, any how Banker 4 is going to deny any proposal as he wants the distribution among 4 bankers where he will be getting 9 ingots as in CASE 3 above. 

And if Banker 5 is eliminated and the case is reduced to CASE 3 where 4 bankers are left then Banker 3 knows he won't be getting anything. So, better he should be happily agree this proposition where he is getting at least 1 ingot.

Finally, offering Banker 5 one more extra ingot than the case where 4 bankers will be left, makes him in favor of this proposition.

Notice that the Banker 5 has to give 3 ingots at least to banker 2 to get his vote as he will be getting 2 ingots in case of 4 bankers as in CASE 3. Whereas, in the same case Banker 3 is not getting anything & would be happily agree if getting 1 ingot at least in this case. 


------------------------------------------------------------------------------

 

Flipping The Unusual Coins

You have three coins. One always comes up heads, one always comes up tails, and one is just a regular coin (has equal change of heads or tails). If you pick one of the coins randomly and flip it twice and get heads twice, what is the chance of flipping heads again?

Chances of flipping head again are - .......% Click to know!