Skip to main content
Posts
Four men and four women are in
Love Island. Each one falls in love with another and is himself/herself
loved by someone else in a complete 8 person loop.
Peter falls in love with a girl who is unfortunately in love with
Albert. Joseph loves a girl who loves the man who loves Elaine. Liza is
loved by the guy who is loved by the girl who is loved by Paolo. Linda
hates Paolo and is hated by the man whom Amy loves.
No guy/guy or girl/girl in Love Island.
Who loves Joseph and whom does Joseph love?
Know here who loves Joseph and Joseph loves whom!
What was the puzzle?
There are few hints given in the question.
-----------------------------------------------------------
1. Peter falls in love with a girl who is unfortunately in love with
Albert.
2. Joseph loves a girl who loves the man who loves Elaine.
3. Liza is
loved by the guy who is loved by the girl who is loved by Paolo.
4. Linda
hates Paolo and is hated by the man whom Amy loves.
-----------------------------------------------------------
STEPS :
STEP 1 :
Let's name all 4 men as M1, M2, M3 and M4 while girls as G1, G2, G3 and G4.
STEP 2 :
Let's start with Peter. He can be at any position M1, M2, M3 or M4. Let's assume that he is at M1. As (1) points M2 must be Albert.
STEP 3 :
As per (2), there are 2 persons in between Joseph and Elaine. That is Joseph can be at M3 or M4 while Elaine can be at G4 or G1 respectively. Exactly, same are possible locations for Paolo and Liza respectively in the loop as (3) suggests.
STEP 4 :
In short, at M3 and M4, we have Joseph and Paolo and G1, G4 are occupied by Liza and Elaine but exact location yet to be known.
STEP 5 :
For The statement (4) to be TRUE, Linda must be hating Paolo.
👉 CASE 5.1 : If Paolo is at M3 then Linda can't be at G2 hence must be at G3. With that, Joseph will be at M4, Elaine at G1, Liza at G4 & only location for Amy as G2.
👉 CASE 5.2 : If Paolo is at M4
then Linda can't be at G3 hence must be at G2. With that, Joseph will be
at M3, Elaine at G4, Liza at G1 & only location for Amy as G3.
CASE 5.1 make other part of the statement (4) false i.e. Linda is hated by man (Paolo here) whom Amy loves is false in the case.
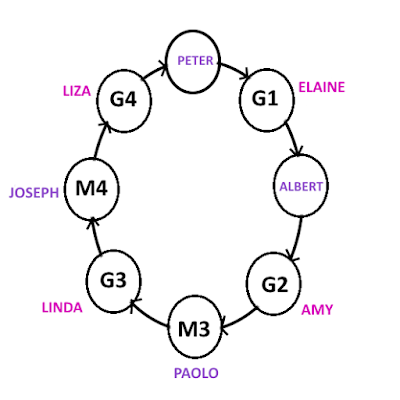
Hence, CASE 5.2 is valid and the final loop looks as -
Finally, turning to the question asked.
Q. Who loves Joseph and whom does Joseph love?
A. Linda loves Joseph and Joseph loves Amy.
Cassie, Jon, Luke, Maria, and
Sahas baked a batch of 36 cookies, two-thirds of which were chocolate
chip. The rest were plain. They each ate at least one right away. The
cookies were so delicious, only one-and-a-half dozen are left, of which
half are plain.
1. Cassie is allergic to chocolate.
2. Luke ate twice as many chocolate chip cookies as plain cookies.
3. Sahas and Maria each ate as many cookies as Luke and Cassie combined.
4. Sahas ate more chocolate chip cookies than Maria.
If all the cookies were eaten by the bakers themselves, how many cookies of each kind did each person eat?
Click here to know the final stats!
What was the puzzle?
Cassie, Jon, Luke, Maria, and Sahas baked a batch of 36 cookies, two-thirds of which were chocolate chip. That means there were 24 chocolate cookies and 12 plain cookies.
The cookies were so delicious, only one-and-a-half dozen are left, of which half are plain. So, 18 cookies are left out of which 9 were plain and other 9 were chocolate.
That is out of 24 chocolate cookies, 24 - 9 = 15 are eaten and out of 12 plain cookies, 12 - 9 = 3 are eaten.
Now, taking a look at the hints given.
1. Cassie is allergic to chocolate.
2. Luke ate twice as many chocolate chip cookies as plain cookies.
3. Sahas and Maria each ate as many cookies as Luke and Cassie combined.
4. Sahas ate more chocolate chip cookies than Maria.
They each ate at least one right away. Since Cassie is allergic to chocolates, must had chosen plain cookie. Luke too must have eaten at least 1 plain cookie otherwise total of cookies eaten by him along with chocolate cookies would be 0.
Sahas and Maria ate same number of cookies but Sahas ate more chocolate cookies than Maria. That means Maria must have eaten more plain cookies than Sahas to balance her number of cookies with the number of cookies eaten by Sahas.
Since there are only 3 plain cookies eaten with 1 of them eaten by Cassie, other 2 must be eaten by Sahas and Luke each while Sahas of Jon had no plain cookies.
With that Luke must had eaten 2 chocolate and 1 plain cookies.
Luke and Cassie together ate to 2 + 1 + 1 = 4 cookies. Hence, Sahas and Maria too ate 4 cookies. Sahas ate 4 chocolate cookies and Maria ate 1 plain and 3 chocolate cookies.
Total of 0 + 2 + 4 + 3 = 9 chocolate cookies eaten by Cassie + Luke + Sahas + Maria together. Hence, rest of chocolate cookies i.e. 15 - 9 = 6 eaten by Jon.
The final stats are -
Cassie : Chocolate - 0 Plain - 1
Luke : Chocolate - 2 Plain - 1
Sahas : Chocolate - 4 Plain - 0
Maria : Chocolate - 3 Plain - 1
Jon : Chocolate - 6 Plain - 0
AJ, Celeste, Juan, Kara, Lily, and Randy all live on Redwood Avenue.
Each of their house numbers has three digits, but the only digits in
their house numbers are 2, 3, 5, and 6. The same digit may appear twice
in one of the addresses.
AJ's house number is Juan's house number doubled.
Juan lives next to Lily and right across from Randy.
Randy's number is the lowest on the street.
Celeste's number is a higher number than AJ's but has the same three
digits as his. They both have the same digit in the hundreds place.
Kara's house number is the reverse of Juan's.
What is each person's street address?
View Answer!
What was the puzzle?
As we know, AJ, Celeste, Juan, Kara, Lily, and Randy all live on Redwood Avenue.
Each of their house numbers has three digits, but the only digits in
their house numbers are 2, 3, 5, and 6 with repetition of digits in house number allowed.
Let's have all the given clues once again here.
1. AJ's house number is Juan's house number doubled.
2. Juan lives next to Lily and right across from Randy.
3. Randy's number is the lowest on the street.
4. Celeste's number is a higher number than AJ's but has the same three
digits as his. They both have the same digit in the hundreds place.
5. Kara's house number is the reverse of Juan's.
STEPS :
1] As per (1), AJ's house number is double of Juan's house number. From the given sets of digits i.e. 2, 3, 5, 6, this is only possible if there is 3 at third place of Juan's house number and 6 at third place of AJ's house number.
That is AJ's house number is XX6 and that of Juan's is XX3.
2] As we can see carry is not being forwarded from Juan's house number XX3 while getting doubled to give AJ's house number. So, it's clear that, the number formed by first two digits of AJ's house number is exactly double of the number formed by first two digits of Juan's house number.
From the given set of digits 2, 3, 5, 6, possible house numbers of AJ and Juan are 666 & 333 or 526 & 263.
If AJ is having house number 666, then as per (4), there would be no valid house number left for Celeste using digits 2, 3, 5, 6.
Therefore, AJ's house number must be 526 and that of Juan's must be 263
3] Now, as per (2), Randy must be having house number 262.
4] As per (4), Celeste's house number must be 5XX. Since, his house number has same digits as that of AJ's but higher than AJ's house number, he must be having house number 562.
5] As per (5), Kara's house number is reverse of Juan's. Therefore, Kara's house number is 362.
6] And as per (2), for the fact that Juan is living next to the Lily to be true, Lily must have house number 265 using the given set of digits 2, 3, 5, 6.
CONCLUSION :
The street addresses of all are listed as below -
AJ : 526, Redwood Avenue.
Celeste : 562, Redwood Avenue.
Juan : 263, Redwood Avenue.
Kara : 362, Redwood Avenue.
Lily : 265, Redwood Avenue.
Randy : 262, Redwood Avenue.
Sam, Alex, Charlie, and Jordan are related.
One of them is the opposite gender from the other three. Here are some facts:
1. Charlie's only son is either Sam or Alex.
2. Jordan's sister is either Alex or Charlie.
3. Jordan is either Sam's brother or Sam's only daughter.
Who is the opposite gender from the other three?
Know here the name of the person with opposite gender!