Process To Identify Fake Coin

What was the task given? 

If we knew, the fake coin is lighter or heavier than original one then the process would have been pretty simple like this! But we don't know.

Let's number the coins from 1 to 12. We'll make 3 groups of these coins as 1,2,3,4 in one group, 5,6,7,8 in other group and 9,10,11,12 in one more group.

First of all weigh 1,2,3,4 against 5,6,7,8.

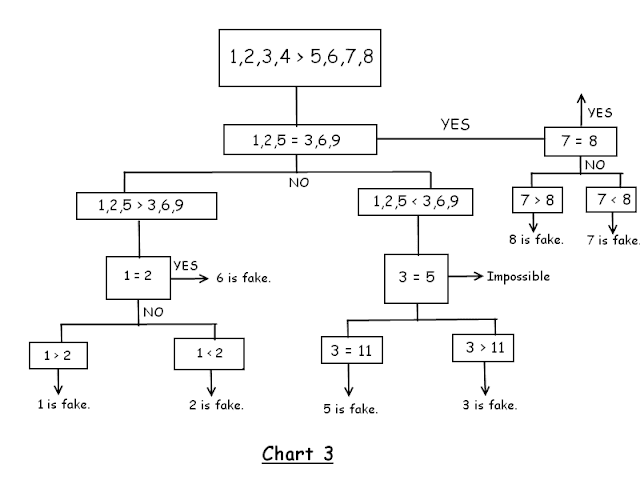
CASE 1 : 1,2,3,4 = 5,6,7,8

 That means coin among 9,10,11,12 is fake one. So weigh 9,10 against 11,8.

   CASE 1.1 : If 9,10 = 11,8 then 12 is fake coin.

   CASE 1.2 : If 9,10 > 11,8 then either 9 or 10 is heavier (hence fake) or 11 is lighter (hence fake). Weigh 9 against 10. If they balance then 11 is fake one. If they don't then heavier of 9 & 10 is fake. 

   CASE 1.3 :  If 9,10 < 11,8 then either 9 or 10 is lighter (hence fake) or 11 is heavier (hence fake). Weigh 9 against 10. If they balance then 11 is fake one. If they don't then lighter of 9 & 10 is fake.
CASE 2 : 1,2,3,4 < 5,6,7,8

This means coins 9,10,11,12 are real ones. So weigh 1,2,5 against 3,6,9. Why these particulars you will know in the process.

  CASE 2.1 : 1,2,5 = 3,6,9

Indicates that either 7 or 8 is heavy of 4 is lighter. So weight 7 against 8. If they balance, then 4 is fake one. If they don't then heavier of 7 & 8 is fake.

   CASE 2.2 : 1,2,5 < 3,6,9

Now 5 can't make this one light or 3 can't make it heavy since 1,2,3,4 < 5,6,7,8. Hence, either 1 or 2 is lighter or 6 is heavier (9 is perfect one). Next weigh 1 against 2. If they balance that means 6 is heavier & hence fake one. If they don't balance then that means 6 is original one & lighter of 1 & 2 is fake.

   CASE 2.3 : 1,2,5 > 3,6,9

Here 1,2 can't make this heavier or 6 can't make it lighter as 1,2,3,4 < 5,6,7,8. Hence either 3 must be lighter or 5 could be heavier. There is no way that 3 & 5 will balance. So skipping this, directly testing 3 or 5 against any good coin say 11.

      CASE 2.3.1 : If 3 = 11 then 5 is fake one.

      CASE 2.3.2 : If 3 < 11 then 3 is fake one. 3 > 11 is impossible as we already deduced that 3 is either lighter one or real one.

CASE 3 : On the similar note, we can deduce fake coin if 1,2,3,4 > 5,6,7,8. The same is depicted in the chart below.

          
To conclude, we need to use balance only 3 times (count number of times it is used in each case) to know the fake coin.