Identifying Number of Truth Tellers in Circle

What was the task given?

Recalling the given situation. 

On a certain island there live only knights, who always tell the truth, and knaves, who always lie.

One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"

 
Every Knight must be surrounded by 2 Knaves and every Knave has to be surrounded by at least one knight to satisfy the given condition. So there must be Knave-Knight-Knave groups must be standing in circle. 

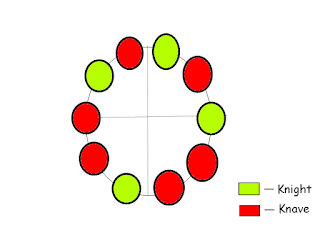
Now if Knave of previous group is counted for the next group, then there will be 5 knights in the circle as shown below.

But the question asks minimum possible number of Knights in the circle.

So after forming 3 groups of Knave-Knight-Knave separately (total 9 in circle), the last person will be obviously surrounded by 2 knaves. Hence, he must be Knight. See below.

This way there can be only 4 knights standing in the circle without violating the given condition.