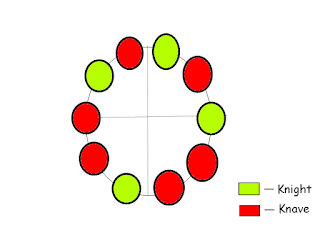
Truth Tellers and Liars in Circle
On a certain island there live only knights, who always tell the truth, and knaves, who always lie.
One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"
Of the 10 in the circle, what is the minimum possible number of knights?
Do you think there can be 5?
One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"
Of the 10 in the circle, what is the minimum possible number of knights?
Do you think there can be 5?