Puzzle : The Fake Coin Challenge!

There are 101 coins out of which 1 is fake, the fake coin is identical to a genuine coin but differs in weight. Using weight balance only twice how can we determine whether the fake coin is heavier or lighter than a genuine coin?

 

 

This is how to do it! 

Fake Vs Genuine Coin Weigh Comparison

This was the challenge!

Remember we are asked to determine whether the fake coin is lighter or heavier when compared with the genuine coin and not to identify the fake coin itself.

Keep aside any one coin. Divide remaining 100 coins into 2 groups of 50 coins each. Put these 2 groups on 2 pans of the balance.

1. If they weigh equal the the coin that is kept aside is fake. Weigh it against any genuine among 100 coins to know whether fake coin is lighter or heavier than genuine.

2. If they are not equal then that means the fake coin either made one side heavier or the other side lighter.

3. Take the heavier group of 50 coins for the next test. Divide them into 2 groups of 25 coins each. 

4. Put 25 - 25 coins on weighing balance. If they weigh equal then that means no fake coin among them which also means the fake coin was in the other group of 50 coins which was lighter in the first weighing. 

Hence, the fake coin is lighter present in the other group of 50 coins making the group slightly lighter compared to group of 50 genuine coins.

4.1. And if the result of weighing 25 - 25 coins is unequal then it's clear that the fake coin is among these 50 coins. Also, it must be heavier making this group to weigh more than the other group of 50 genuine coins in the first weighing.

This way, we can determine whether the fake coin is heavier or lighter than genuine one using the weighing balance only twice.

The Bookworm's Move

There are three books on a shelf standing side by side as they are normally placed on bookshelf. Each book is 10ml thick. The bookworm eats its way through the first page of the first book to the last page of the last book.

How far did the bookworm move if it can only move in a straight horizontal line?

30 mm? It must have moved only 10mm! 

Tricky Data of Bookworm's Movement

What was the data given?

Yes, bookworm only moved 10 mm distance. Read the given data given once again. 

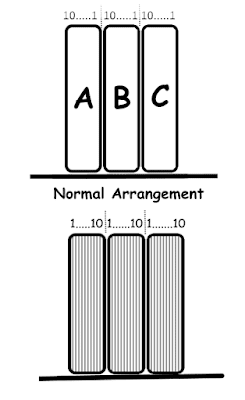
Books are arranged in the way we normally place on the shelf. Normally, they are placed in such a way that the their spines (where most of books have name) are easily visible to us. 

If A, B and C are books having 10 pages each then with the normal placement the pages would count from 10 to 1 if counted from left to right. 

In other arrangement, they would count from 1 to 10 if counted from left to right.

See below.

Now, as per data given, the books are arranged in normal way on the shelf and the bookworm started from first page of first book to the last page of last book.
That is it must have ate only middle book which is 10 mm wide.

Hence, the bookworm must have moved only 10 mm.

Story of Man Having 2 Girlfriends

A man who lives in Middletown has two girlfriends, one in Northtown and one in Southtown. 

Trains from the Middletown train station leave for Northtown once every hour. Separate trains from the station also leave for Southtown once every hour. No trains go to both Northtown and Southtown.

Each day he gets to the Middletown train station at a completely random time and gets onto the first train that is going to either Northtown or Southtown, whichever comes first.

After a few months, he realizes that he spends 80% of his days with his girlfriend from Northtown, and only 20% of his days with his girlfriend from Southtown.

How could this be?

THIS could be the reason behind it! 

Behind Unfair The Number of Visits

What's the story behind the title?

The man arrives at Middletown train station at a completely random time of the day. 

Let's take a look at what happens when he arrives at random time of the day.

After arrival on the station, he is likely to get the train in next hour for sure.

After arriving at random time, there are 80% chances that the first train arriving at the station is heading towards Northtown and 20% chances are there the train is heading towards the Southtown. 

That is there has to be 80% minutes of hour (80% of 60 = 48 minutes) where the first train after is heading towards Northtown and 20% minutes of hour where the next train is heading towards Southtown (20% of 60 = 12 minutes).

So, the trains heading towards the Southtown must be scheduled 12 minutes apart from train heading towards the Northtown.

For example, if trains heading to Northtown are scheduled at 9:00 AM, 10:00 AM, 11:00 AM.......etc then the trains to the Southtown must be scheduled at 9:12 AM, 10:12 AM, 11:12 AM.....etc.

With arrival in 48 minutes past 9:12 AM, 10:12 AM etc, he must be getting the Northtown train and if arrived in 12 minutes past 9:00 AM,10:00 AM etc, he would be getting the Southwest train.

Remember, the timing given are for examples only. The Northwest trains may be scheduled at 9:48 AM, 10:48 AM,......etc and Southwest may be scheduled at 10:00 AM, 11:00 AM.

Key is they leave 12 minutes apart, so that 60 minutes of hour are divided into 48 minutes ahead of Northwest train and 12 minutes ahead of Southwest train. 

Will the Sheep Survive?

Hundred tigers and one sheep are put on a magic island that only has grass. Tigers can live on grass, but they want to eat sheep. If a Tiger bites the Sheep then it will become a sheep itself. If 2 tigers attack a sheep, only the first tiger to bite converts into a sheep. Tigers don’t mind being a sheep, but they have a risk of getting eaten by another tiger.

All tigers are intelligent and want to survive. 

Will the sheep survive?

Survival chances of the sheep are - Click Here! 

Survival Chances of the Sheep

Why sheep is in danger?

First let's see what happens when there are different number of tigers present on 
the island. Remember we are talking about survival of the sheep that is initially present n the island and not sheep converted from tiger.

1. Suppose there are only 1 tiger and 1 sheep on the island. Then, the tiger will eat 
    the sheep and won't have fear of being eaten up after transformation into sheep 
    as there is not tiger left. 

    The sheep will not survive.

2. Let's suppose there are 2 tigers and 1 sheep present. Each intelligent tiger can think - 

    ----------------------------------------------------------------------------------------------------------
   "If I eat a sheep then I will be converted into sheep and other tiger would eat me
    as it would result into '1 tiger and 1 sheep' scenario above in (1). 

    So, I should not take risk"
    ---------------------------------------------------------------------------------------------------------- 

    The sheep will be survived.


3. Now suppose there are 3 tigers and 1 sheep are on the island. Each tiger would think-  
     ----------------------------------------------------------------------------------------------------------
    "If I target the sheep and get converted into sheep itself then on the island there
     would be 2 tigers and 1 sheep as above case (2). 

     As per that, none of other 2 tiger would dare to attack me and I would be 
     survived as a sheep in the end. 

     So better I should attack the sheep and anyhow I will be survived in the end as a
     sheep"
     ----------------------------------------------------------------------------------------------------------
      The sheep will not survive.

4. Finally, suppose there are 4 tigers and 1 sheep. Now, each tiger can put logic like -       ----------------------------------------------------------------------------------------------------------
    "If I attack the only sheep and get myself converted to sheep then this case 
     will be reduced to '3 tigers and 1 sheep' as in case (3). 

     In that case, the sheep has 0 chance of survival in the end. 

     That means, my life will be in danger as in above case (3), if I attack 
     this sheep toget converted into sheep. Better, I shouldn't attack"
     ----------------------------------------------------------------------------------------------------------
     The sheep will be survived.

Conclusion : 

If observed carefully, it can be concluded that the sheep will be survived when there are EVEN number of tigers (Case 2 and Case 4) are present. And obviously, will be in danger when there are ODD number of tigers present on the island.

In the given situation, there are 100 tigers on the island which is EVEN number. That means, as per above conclusion the only sheep on the island will be survived.

 

Simple Logical Mathamatical Problem

There are 5 people who can build 5 houses in just 5 days.
 
How long would it take 100 people to build 100 houses?

100? Really? Check back or click here!

Answer Of Simple Logical Mathematical Problem

Want to read the question first? 

Did you answer 100?

"There are 5 people who can build 5 houses in just 5 days."

The above statement suggests that 1 man takes 5 days to build 1 house & not 1 man take 1 day to construct 1 house.

So 100 people will make 100 houses in only 5 days as each one completing the task in 5 days!

Trip Around The Earth

Professor Fukano plans to circumnavigate the world in his new airplane. But the plane's fuel tank doesn't hold enough for the trip—in fact, it holds only enough for half the trip. But with the help of two identical support planes (which can refuel him in mid-air) piloted by his assistants Fugari and Orokana, the professor thinks he can make it in one trip. But since all three planes have the same problem of limited fuel, how can they work together to achieve the professor's goal without anyone running out of fuel?

1. The professor's plane must make a single continuous trip around the world without landing or turning around.

2. Each plane can travel exactly 1 degree of longitude in 1 minute for every kiloliter of fuel. Each can hold a maximum of 180 kiloliters of fuel.

3. Any plane can refuel any of the others in mid-air by meeting at the same point and instantly transferring any amount of fuel.

4. Fugari and Orokana's planes can turn around instantaneously without burning fuel.

5. Only one airport is available for any of the planes to land, take off, or refuel.

6. All three planes must survive the experiment, and none may run of fuel in mid-air.

'This' is how mission is completed!
  

For The Journey Around The Earth

First read T&Cs of the journey! 

Let's assume that the only airport mentioned is located at the top of the earth. 

Recollect all the data given.
----------------------------------------------------------------------------

1. The professor's plane must make a single continuous trip around the world without landing or turning around.

2. Each plane can travel exactly 1 degree of longitude in 1 minute for every kiloliter of fuel. Each can hold a maximum of 180 kiloliters of fuel.

3. Any plane can refuel any of the others in mid-air by meeting at the same point and instantly transferring any amount of fuel.

4. Fugari and Orokana's planes can turn around instantaneously without burning fuel.

5. Only one airport is available for any of the planes to land, take off, or refuel.

6. All three planes must survive the experiment, and none may run of fuel in mid-air.

------------------------------------------------------------------------------

As per (2), since each plane travel 1 degree of longitude in 1 minute for every kiloliter of fuel, means that plane need 360 minutes (6 hours) and 360 kiloliters of fuel. But remember plane can hold only 180 kiloliters of fuel.

Let's suppose that, all three planes takes off from airport exactly at 12:00 PM towards the WEST.

We will break this 6 hours journey into 8 parts where each plane travels 45 degree of longitude east or west using 45 kiloliters of fuel.  

START :

--------------------------------------------------------------------------------

PART 1 :

 Exactly at 12:45 PM, all will be at 45 degree angle with reference to the center of the earth.
At this point, each of them will use 45 kiloliters of fuel. Hence, each will have 135 kiloliters of fuel. Here, Orokana gives away 45 kiloliters to each of Fukano & Fugari. So she is left with the 45 kiloliters which she uses to go back to the starting point.

 
---------------------------------------------------------------------------------

PART 2 : 

In next 45 minutes, both Fukano and Fugari moves to 90 degree of longitude spending 45 kiloliters of fuel. Now,here both will have 135 kiloliters each in their fuel tank. Here, Fugari refuels Fukano's fuel tank with 45 kiloliters of fuel; leaving 90 kiloliters in own tank for the backward journey towards the starting point.

---------------------------------------------------------------------------------

PART 3 : 

Fukano travels further, while Fugari is in midway of the backward journey. Again, both spend 45 kiloliters of fuel.

 
----------------------------------------------------------------------------

PART 4 :

Exactly at 3:00 PM, Fukano reaches at 180 degree while Fugari reaches back to the starting point. Till then, Orokana refuels her plane & takes off towards EAST. She has to take off as Fukano is left with only 90 kiloliters of fuel by which he could travel half of the rest of journey.

-----------------------------------------------------------------------------

PART 5 :

In next 45 minutes, Fukano's plane uses 45 kiloliters further while Orokana travels 1/3rd of Fukano's remaining journey in reverse direction so as to meet Fukano in midway. In process, her plane again uses 45 kiloliters of fuel with 135 kiloliters left.

--------------------------------------------------------------------------------

PART 6 :

At 04:30 PM, Orokana meets Fukano whose plane had no fuel left at the point & refuels his plane with 45 kiloliters of fuel. Remember Orokana's plane consumed 45 kiloliters more till she meets Fukano. Now, since both of them have left only 45 kiloliters in fuel tank, Fugari whose plane standing at airport is refueled at full 180 kiloliters takes of in the direction of EAST.

----------------------------------------------------------------------------------

PART 7 : 

At 05:15 PM, when fuel tank indicators of both Fukano & Orokana are pointing to 0, Fugari meets them & gives 45 (to Fukano) + 45 (to Orokana)  = 90 out of 135 (180 - 45 used since take off) . Now all are left with 45 kiloliters of fuel & 45 degrees of journey is left.

----------------------------------------------------------------------------------

PART 8 : 

And this is how, exactly at 06:00 PM all of them reaches back to the starting point safely.

But is this the most efficient way to make trip around the Earth? Certainly not! 

If plane was built with fuel tank of 360 + then the mission wouldn't have required any assistance. Just because of limited fuel tank, 45 + 45 + 90 + 90 + 90 + 90 + 45 + 45 = 270 Kiloliters of fuel burnt to assist Fukano's plane.

The Green-Eyed Logic Puzzle

In the green-eyed logic puzzle, there is an island of 100 perfectly logical prisoners who have green eyes—but they don't know that. They have been trapped on the island since birth, have never seen a mirror, and have never discussed their eye color.

On the island, green-eyed people are allowed to leave, but only if they go alone, at night, to a guard booth, where the guard will examine eye color and either let the person go (green eyes) or throw them in the volcano (non-green eyes). The people don't know their own eye color; they can never discuss or learn their own eye color; they can only leave at night; and they are given only a single hint when someone from the outside visits the island. That's a tough life!

One day, a visitor comes to the island. The visitor tells the prisoners: "At least one of you has green eyes." 

On the 100th morning after, all the prisoners are gone, all having asked to leave on the night before. 

How did they figure it out?


Here is the solution! 

The Green-Eyed Puzzle Solution

Here is that Puzzle! 

Nobody is going to dare to go the guard unless he is absolutely sure that he is green eyed; otherwise it would be suicidal move.

-------------------------------------------------------------------------------------
 
For a moment, let's assume there are only 2 prisoners named A & B trapped on island.

On first day, A is watching green eyed B & B can see green-eyed A. But both are not sure what is color of their own eyes. Instead, A(or B) waited B(or A) to escape from island since he is green-eyed. Rather both are sure that other too doesn't know anything about color of own eyes.

On next morning both see each other still on island. Here is what A thinks.

If I was non green-eyed then B would have realized that the person pointed by visitor in his statement ('at least one of you have green eyes') is himself. Hence, B would have realized that he is green-eyed & could have escaped easily. Since B didn't try to escape that means I too must have green eyes.

So A can conclude that he too have green eyes. Exactly same way, B concludes that he too has green eyes. Hence, on next day both can escape from the island.
 
Note that, if the night of the day on which visitor made statement is counted then next day would have 1st morning & 2nd night since visitor's visit. Now since A & B left on 2nd night, we can't see anybody on 2nd morning next day.

--------------------------------------------------------------------------------
 
Now let's assume there are 3 prisoners named A,B and C trapped on island.

Let's think from A's point of view as an example.What he thinks.

Let me assume I don't have green eyes.Now each B and C could see 1 green-eyed & other non green-eyed person. But still they don't know color of own eyes.So on that night nobody tries to escape.

On first morning I see both B and C still present there.

Now B can think that if he has no green eyes then C could have concluded that the person pointed by visitor's statement ('at least one of you have green eyes') is C himself (as both A & B are non green-eyed. This way, C would have realized that he is green-eyed.

In a very similar way, B would have realized that he too is green-eyed.

Now both of them could have escaped on that night as they are sure that they are green-eyed.

But on the second morning, I see again both of them are still there. So now I can conclude that I too have green eyes.

If A can conclude then why can't B and C?  So after seeing each other on 3rd day, each of 3 can conclude color of eyes is green. Now on 3rd night they all can escape safely.

This is called as inductive logic.

-------------------------------------------------------------------------------

If observed carefully, 2 prisoners need 2 nights and 3 prisoners need 3 nights to logically deduce that the each of them is green-eyed.

Hence, 100 prisoners would require 100 nights to absolutely make sure that each of them is green eyed.

That's why on the 100th morning day, there is no prisoner present on island. 

The Hiker's Dilemma

A hiker comes across an intersection where three roads cross. He looks for the sign indicating the direction to his destination city. He finds that the pole carrying three city names and arrows pointing to them has fallen. He picks it up, considers it, and pops it back into place, pointing out the correct direction for his destination. How did he do it?

This is how he did it!

Hiker Got The Right Direction

What was the dilemma? 

Since he knew very well from which city he came; he just oriented that arrow in right direction. And obviously hence rest of all arrows are pointed in the right directions as well. This is how he found his right way!

Water Measured Using 2 Buckets - Puzzle Cracked

What was the challenge? 

Method 1 :

1. Fill up the 3 gallons bucket & pour into 5 gallons bucket.

2. Again fill the gallon bucket & once again pour it into 5 gallons bucket. After completely filling 5 gallons bucket there will be 1 gallon left in 3 gallons bucket.

3. Empty 5 gallons bucket.

4. Pour that 1 gallon into 5 gallons bucket. Now fill up 3 gallons bucket. We have 4 gallons of water now 1 in 5 gallons bucket & 3 in 3 gallons bucket.


Method 2:

1. Fill up 5 gallons bucket & pour it into 3 gallons bucket. 2 gallons would remain in 5 gallons bucket.

2. Pour that 2 gallons of water into 3 gallons bucket. Now only space for 1 gallon left in 3 gallons bucket.

3. Again fill up 5 gallons bucket & pour into 3 gallons bucket containing 2 gallons of water left. So only 1 gallon can be poured & 4 gallons would be remaining in 5 gallons bucket.