A Long Journey of 27000 Miles

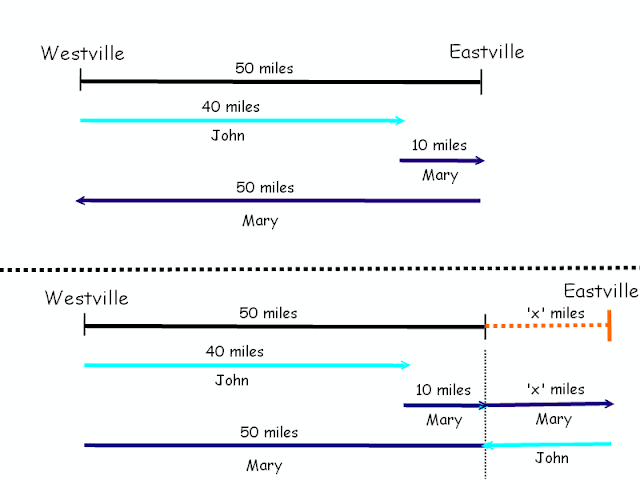
The MacDonalds are planning a long car journey of 27,000 miles. If they use tires that last 12,000 miles each, how many tires will they need, and how can they make the best use of them?

This is how usage of tires can be optimized!

Optimizing The Use of Tires in Long Journey!

How long the actual journey is?

Since each tire would be traveling 27,000 miles, when car travels 27000 miles; tire -miles are equal to 27000 x 4 = 108000.

But the each tire lasts for 12000 then tires required = 108000/ 12000 = 9.

Now managing use of these 9 tires need some planning.

For first 12000 miles of 27000 miles they can use 4 out of 9 tires. For the rest of 15000 miles use of remaining 5 tires need to be planned.

Best way is to change 1 tire after every 3000 miles like below.

First 3000 miles: Tires 1, 2, 3, 4

Second 3000 miles: Tires 2, 3, 4, 5

Third 3000 miles: Tires 3, 4, 5, 1

Fourth 3000 miles: Tires 4, 5, 1, 2

Fifth 3000 miles: Tires 5, 1, 2, 3

This way, it's made sure that each tire is used for only 12000 miles. And this is how the journey can be completed using 9 tires only.

Sharing The Driving Time!

John and Mary drive from Westville to Eastville. John drives the first 40 miles, and Mary drives the rest of the way. That afternoon they return by the same route, with John driving the first leg and Mary driving the last 50 miles.

Who drives the farthest, and by what distance?

'This' is the person who drives the farthest!


Source

Uneven Sharing of Driving Time!

But actual how it was shared?

Let's assume for a moment, the distance between Westville and Eastville is 50 miles.

In this case, John drives only 40 miles while Mary drives 10 + 50 = 60 miles. For any distance beyond 50 miles, Mary drives east equal distance as John drives west.

So in any case the difference will remain same of 20 miles. So Mary drives the farthest by 20 miles.

Sara's Desert Trek

Sara needs to trek from an oasis to a destination 10 miles away across a barren desert. 

The facts:

• Crossing one mile of desert requires using 1 gallon of water.
• Sara can only carry 6 gallons of water at a time.
• Sara can drop a water cache (of any amount of water from the supply she is carrying at that moment) at any of the nine stops along the route, and then pick up any part of the cache on a later trip.

What's the minimum number of times Sara must leave the oasis in order to cross the entire 10 mile span of desert?

This is how she optimizes her journey! 

Sara's Planning in Desert Trek

What was the challenge in journey?

1. First Sara collects 12 gallons of water at milepost 1 after having 3 trips from source. She uses 2 gallons (out of 6) for forward & backward journey from source to milepost & dropping 4 gallons in cache at milepost 1.

2.She collect 6 gallons more water at the start of 4th trip from source & drops 5 gallons at milepost 1. Now, she doesn't need to return back to source and 17 gallons of water available at milepost 1.

3.In next 2 rounds, she moves 8 gallons of water from milepost 1 to milepost 2 (1 for forward + 4 for drop + 1 for backward journey in each round). 

4.Now only 5 gallons left at milepost 2. She uses 1 gallon for journey from milepost 1 to milepost 2 and drop remaining 4 gallons at milepost 2. Now, 12 gallons of water is available at milepost 2.

3.Next, using 2 gallons (out of 6 which is maximum she can carry) she moves from milepost 2 to milepost 4 and drop 2 gallons at milepost 4 & comes back at milepost 2 using remaining 2. 

4. Again, on arriving back at milepost 2, she has left with 6 gallons of water at milepost 2 out of which she uses 2 to reach milepost 4 where 2 gallons of water still available there already collected in previous round. Now, she doesn't need to return back from
milepost 4.

5. She uses the remaining 6 gallons of water to reach at the milepost 10.

To conclude, Sara has to leave Oasis only 4 times as describe in steps 1 and 2 if she want to cross the entire 10 mile span of desert.  

Journey In Parts

Someone drove from Aardvark to Beeville.

On the first, day they traveled 1/3 of the distance.

On day two, they traveled 1/2 of the remaining distance.

On day three, they traveled 2/3 of the remaining distance.

On day four, after covering 3/4 of the remaining distance, they were still 5 miles away from Beeville.

How many miles had they covered so far?

Know the total distance traveled!
 

Total Distance In The Journey

Click for the question! 

We need to start in reverse.

In last part after covering 3/4 still 5 miles left which accounts for 1/4 of remaining distance. Hence, 20 miles were left at the start of DAY 4.

On DAY 3, 2/3rd covered leaving 20 miles for DAY 4. That means 20 miles distance is remaining 1/3rd. Hence, at the start of DAY 3, 60 miles were left.

On DAY 2, 1/2 of covered leaving 60 miles for DAY 2. So that means 60 miles distance is remaining 1/2. So at the start of DAY 2, 120 miles yet to be covered.

On DAY 1, 1/3 of covered leaving 120 miles for DAY 2. Meaning 120 miles distance is remaining 2/3. Hence, 180 miles yet to be covered at the start of DAY 1.

Out of 180 miles, 175 covered in 4 days still 5 miles left.

A Check Post At Each Mile

A poor villager grows mango in his land and sells them in the town. The town is 1000 miles away from the village. He has rented a truck for transporting the mangoes to the town. The truck can carry 1000 mangoes at one time and this season, he was able to yield 3000 mangoes.

There is a problem. At each mile till the town, there is a check post at which he must give one mango each while traveling towards the town. However, if he is traveling from the town towards his village, he won’t have to give anything.

Transportation Truck

Tell a way in which the villager can take highest possible number of mangoes to the town.

Know here that highest possible number!

Source 

Smart Saving At Check Posts

How much each check post charging?

Obviously, he can't make 3 trips from town to village straightaway as in that case he wouldn't have anything left (3 x 1000 mangoes paid).

So he need to divide the journey into parts. While breaking journey into parts he has to make sure that after each part he will need less trips to complete the next part.

Now if somehow he pays 1000 mangoes in first part of the journey then for next part he has to make only 2 trips to carry 2000 mangoes.

Part 1 : Hence, he should first make 3 trips till 333 miles. In this part, he would pay 3 x 333 = 999 mangoes leaving 3000 - 999 = 2001 mangoes in stock.

Part : 1

Part 2 : He should leave 1 mango here & take 2000 mangoes further. For next part, he need to make at least 2 trips for 2000 mangoes. In order to save number of trips in next part some how he need to make mangoes in stock less than 1000. For that he should make 2 trips 500 mile further. So he will pay 2 x 500 = 1000 mangoes but having 2000 - 1000 = 1000 mangoes in stock. Still he has to travel 1000 - 500 - 337 = 167 miles.

Part : 2

Part 3 : For next 167 miles, he need to make only 1 trip of 1000 mangoes where he will pay 167 mangoes leaving 1000 - 167 = 833 mangoes. 

Part : 3

This is how he can save 833 mangoes in entire journey.