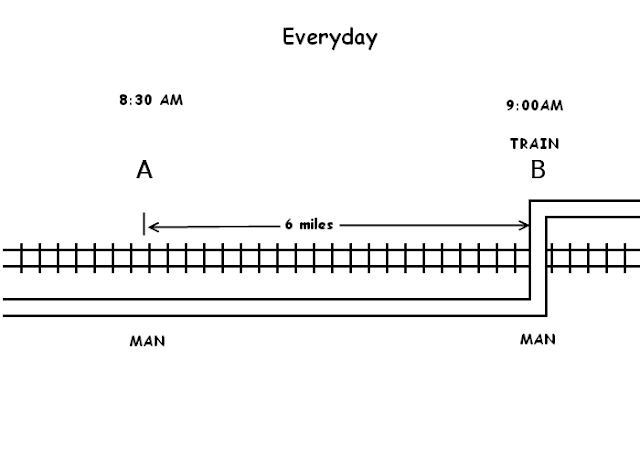
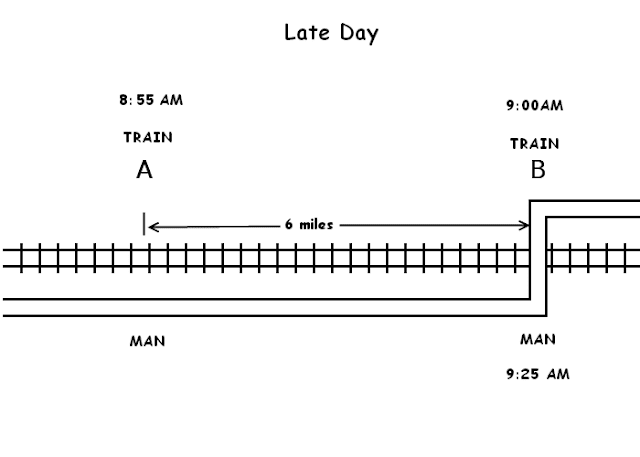
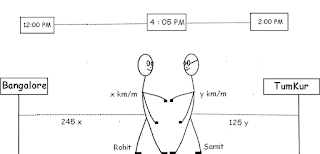
How Far Did I Run?

I leave my front door, run on a level road for some distance, then run to the top of a hill and return home by the same route. I run 8 mph on level ground, 6 mph uphill, and 12 mph downhill. 

If my total trip took 2 hours, how far did I run?

I ran the distance.....Click here for more!

Calculation of Avarage Speed is Tricky!

First read what was the question!

Let's first find my average speed when I was running uphill & downhill.

Assume 'x' be the distance that I have to run to reach at the top of the hill in time 'y'.

So x/y = 6 mph.

While running downhill, I cover same distance 'x' in time 'y/2' as I ran at double speed of 12 mph.

Average speed = Total Distance / Total Time

Average speed = (x + x) / (y + y/2)

Average speed = (4/3)(x/y)

Average speed = (4/3) x 6

Average speed = 8 mph.

That means my average speed on hill is equal to the my speed on level ground and that is 8 mph.

Since I ran for 2 hours in my trip the distance I ran is 8 x 2 = 16 miles.

The Hiker's Dilemma

A hiker comes across an intersection where three roads cross. He looks for the sign indicating the direction to his destination city. He finds that the pole carrying three city names and arrows pointing to them has fallen. He picks it up, considers it, and pops it back into place, pointing out the correct direction for his destination. How did he do it?

This is how he did it!

Hiker Got The Right Direction

What was the dilemma? 

Since he knew very well from which city he came; he just oriented that arrow in right direction. And obviously hence rest of all arrows are pointed in the right directions as well. This is how he found his right way!

A Railway And Cyclist Crossing

A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. 

What was the speed of the train?

Skip To Know The Speed Of The Train! 

To Cross The Cyclist...

What was the scenario?

 Let's suppose he reaches the crossing at 9:00 AM. Usually at 8:30 AM he is at point A, 6 miles before the usual crossing point B (speed of 12 mph, means 6 mile per half hour).

On the day on which he was late by 25 minutes, he must be again at point A (i.e. 6 miles ahead of usual crossing point B) at 8:55 AM. So at this point, both train and man were at the same point A. And the train as everyday, reaches point B at 9:00 AM. That means, it travels 6 miles in 5 minutes. Hence, train must be traveling at 72 mph.  

Time Of Arrival?

One day Rohit decided to walk all the way from city Bangalore to Tumkur. He started exactly at noon. And Samit in city Tumkur decided to walk all the way to Bangalore from Tumkur and he started exactly at 2 P.M. on the same day.

Both met on the Bangalore - Tumkur Road at five past four, and both reached their corresponding destination at exactly the same time.

At what time did we both arrive?

      Beginning of Journey

Find here their arrival time! 

Finding The Time Of Arrival

What was the puzzle? 

Let 'x' km/minute be the speed of Rohit's walk. He started to walk at 12 PM & met Samit at 4:05 PM. That means he has walked for 245 minutes. 

Distance traveled by Rohit = 245x km

Let 'y' km/minute be the speed of Samit's walk. He started to walk at 2 PM & met Samit at 4:05 PM. That means he has walked for 125 minutes.

Distance traveled by Samit = 125y km 

    Time of Meeting

Now after meeting each other they resumed their journey further. That means Rohit continues to Tumkur & covers distance of 125y km at his speed of x km/minute. Time taken by him further to complete the journey is 125y / x minutes (Time = Distance/Speed).