Skip to main content
Posts
On a certain island there live only knights, who always tell the truth, and knaves, who always lie.
One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"
Of the 10 in the circle, what is the minimum possible number of knights?
Do you think there can be 5?
What was the task given?
Recalling the given situation.
On a certain island there live only knights, who always tell the truth, and knaves, who always lie.
One day you find 10 island natives standing in a circle. Each one states: "Both people next to me are knaves!"
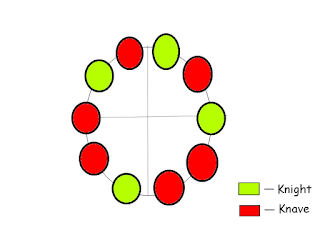
Every Knight must be surrounded by 2 Knaves and every Knave has to be surrounded by at least one knight to satisfy the given condition. So there must be Knave-Knight-Knave groups must be standing in circle.
Now if Knave of previous group is counted for the next group, then there will be 5 knights in the circle as shown below.
But the question asks minimum possible number of Knights in the circle.
So after forming 3 groups of Knave-Knight-Knave separately (total 9 in circle), the last person will be obviously surrounded by 2 knaves. Hence, he must be Knight. See below.
This way there can be only 4 knights standing in the circle without violating the given condition.