Which way is the bus going? Left or Right?

Can you guess in which direction this bus is going?

Are you in the right direction?

Bus is Moving In 'This' Direction!

Why dirction was asked to find? 


Well, it totally depends on the location of the bus. How? Read further.

If you look at it carefully, then you can notice that the doors of the bus are missing.
That clearly indicates, those must be on the other side of bus.

Hence if bus is on the roads of India then it must have doors at it's left side & hence the bus must be moving in the right direction.

While in some countries, bus might have doors at the right; in the case the bus must be moving in left direction. 

Viral Maths Problem Confusing Students & Parents

There are 73 red, blue and green marbles in a jar. There are twice as many red marbles as blue marbles. There are 19 more marbles than green marbles. 

How many green marbles are there?

Check if you are correct! 

Solution of Viral Maths Problem Confusing Students & Parents

What was the problem?

Using Algebra : 

Let r,b and g be the numbers of red, blue and green marbles in the jar.

There are 73 red, blue and green marbles in a jar.

So r + b + g = 73    .....(1)

There are twice as many red marbles as blue marbles.

r = 2b                  ......(2)

There are 19 more blue marbles than green marbles. 

b = g + 19            

g = b - 19            ......(3)

Putting (2) and (3) in (1), gives

2b + b + b - 19 = 73

4b = 92

b = 23

Putting b = 23 in (3) gives,

g = 23 - 19 = 4

Putting  b = 23 in (2), gives 

r = 2x23 = 46

So there are 46 red,23 blue and 4 green marbles in the jar.

Without Algebra :

In the case, we need to try trail and error method.

If g = 1, then b = 20 and r = 2(20) = 40 giving total 40 + 20 + 1 = 61.

If g = 2, then b = 21 and r = 2(21) = 42 giving total 42 + 21 + 2 = 65.

If g = 3, then b = 22 and r = 2(22) = 44 giving total 44 + 22 + 3 = 69.

Total is increasing at the rate of 4. So finally,

If g = 4, then b = 23 and r = 2(23) = 46 giving total 46 + 23 + 4 = 73.


So there are 46 red,23 blue and 4 green marbles in the jar.

The Buyer Who is Thief

Once a man steals Rs.100 note from the shop. Later he purchases good of worth Rs.70 from the same shop using that note. The shopkeeper gives back Rs.30 in return. 

How much did shopkeeper loose in the case?


Do you think Rs.130? Or anything else? 

Loss Due To Thief Buyer

What's the case history? 

So did you just answer Rs.130 ? No, that's not correct!

Thief initially steals Rs.100 note. Now imagine instead of Rs.100 he steals goods of worth Rs. 70 + Rs.30 (given by shopkeeper). So eventually, the shopkeeper lost only Rs.100 in the process. 

In other words, the thief exchanges Rs.70 with the goods in the case. He pays for those goods to shopkeeper. So he looses Rs.70 from stolen Rs.100 & gains back via goods.

So eventually, the shopkeeper lost only Rs.100 in the case.

 

The Exact Age?

Tommy: "How old are you, Mamma?"

Mamma: "Let me think, Tommy. Well, our three ages add up to exactly seventy years."

Tommy: "That's a lot, isn't it? And how old are you, Papa?"

Papa: "Just six times as old as you, my son."

Tommy: "Shall I ever be half as old as you, Papa?"

Papa: "Yes, Tommy; and when that happens our three ages will add up to exactly twice as much as to-day."

Tommy: "And supposing I was born before you, Papa; and supposing Mamma had forgot all about it, and hadn't been at home when I came; and supposing..."

Mamma: "Supposing, Tommy, we talk about bed. Come along, darling. You'll have a headache."

Now, if Tommy had been some years older he might have calculated the exact ages of his parents from the information they had given him. Can you find out the exact age of Mamma?

Here is CALCULATION of exact age!

Calculation Of The Exact Age

What was the problem? 

Let us suppose T be the age of Tommy, M be of the Mamma and P be that of Papa.

Sum of their ages is 70.

T + M + P = 70  ......(1)

and Papa is 6 times as old as Tommy,

P = 6T  .....(2)

In unknown number of years X, Papa will be twice old as Tommy,

P + X = 2 (T + X)  ....(3)

and the sum of ages at that time is 70 x 2 = 140,

(T + X) + (P + X) + (M + X) = 140.

T + P + M + 3X = 140

From (1), above equation becomes,

70 + 3X = 140

X = 70/3     .....(4)

Putting (4) and (2) in (3),

P + X = 2 (T + X) 

6T + 70/3 = 2(T + 70/3)

T = 70/12    .....(6)

Using (6) in (2),

P = 6T

P = 6(70/12)

P = 70/2    ......(7)

Putting (6) and (7) in (1),

M = 70 - 70/2 - 70/12

M = 29.1666 = 29 years 2 months.

P = 70/2 = 35 years.

T = 70/12 = 5.8333 = 5 years 10 months.

 
To summarize, the Tommy is 5 years 10 months old, Mama is 29 years 2 months old and Papa is 35 years old.

50th Fastest And The 50th Slowest

Matt is the fiftieth fastest and the fiftieth slowest runner in his school.

Assuming no two runners are the same speed, how many runners are in Matt’s school?

Find here total number of runners! 

Total Runners In The School

Read the given data first!
 
This could be very tricky one. Let's assume that the Matt is fifth fastest and fifth slowest runner in his school.

Then there are 4 runners ahead of him numbered 1 to 4 and 4 behind him numbered 6 to 9. So there would be total 9 runners in his school in the case.

But Matt is 50th fastest runner meaning 49 are ahead of him numbered 1 to 49. And 49 are behind him numbered as 51 to 99 (total 49) while Matt is at 50th position.

Hence, there are 49 + 1 + 49 = 99 runners in his school.

A Rich Earl And Swamp

A rich earl has become the owner of a piece of land, which to his dissatisfaction turned out to be nothing more than a big swamp. The earl wants to get rid of the swamp. 

A salesman advises him to use his fast-growing plants which can cover the swamp very quickly. "This plant doubles every day, tomorrow you will have two, the day after tomorrow four, etc. In 80 days, your swamp will be completely covered." The earl reacts: "80 days? This takes far too much time. Then just give me eight of these plants."

Question 1: What did the earl think?

Question 2: And what do you think?

Go to the answers directly!

Planting Trees Covering Swamp

What's the exact story? 

The earl must have thought that planting 8 trees on first day itself would cause him to wait for only 10 days. That's totally wrong conclusion.

Though started with 8 trees, on other day number will be doubled only not tripled or increased to x8. Starting with 8 trees is like skipping 3 days (2,4,8) if started with 1 tree.That is only 3 days would be saved. 

In short, with 8 plants, the earl need to wait for 77 days!   

Strange Creatures on Island

There are people and strange monkeys on this island, and you can not tell who is who (Edit: until you understand what they said - see below). They speak either only the truth or only lies.

Who are the following two guys?

A: B is a lying monkey. I am human.

B: A is telling the truth.

Know who are they! 

 

Identifying the Strange Creature

What was the situation?

 Let's first have statements by 2 creatures - 

A: B is a lying monkey. I am human.

B: A is telling the truth.

If we assume B is telling the truth then A is also telling the truth. But A in statement says B is lying which contradicts our assumption. 

Hence, B must be lying. If B is lying then statement of B suggest that A is also must be lying. That mean 'B is lying monkey' part of statement made by A is too lie. Since we have deduced already B is lying, the lying statement of A suggests that B is not monkey. Hence B is the lying man!

Other lie spoken by A is that it is human. Hence A must be a lying monkey! 

 

Forgotten Bank Account Number

Today, John has to transfer 50 euro to the bank account of a Dutch friend. He has written down the account number on a piece paper. But since he had forgotten to take out the paper from his trousers when he put them in the washing machine, one digit of the bank account number became unreadable. The note says: 3170?4847. 

The friend of John is climbing the Mount Everest at the moment, so it is impossible for John to call his friend. Suddenly he remembers that a for a valid Dutch bank account number it holds that the first digit times 9 + the second digit times 8 + the third digit times 7 + ...... + the ninth digit times 1 should be divisible by 11. John thinks for a moment and finds the correct number. 

What is it? 

That it is !

Recalling Forgotten Bank Account Number

What were the clues? 

Let x be that missing digit. Then the bank account number looks like, 3170x4847.

Now 9 x First Digit + 8 x Second Digit + 7 x Third Digit.......must be divisible by 11.

That is 27 + 8 + 49 + 0 + 5x + 16 + 24 + 8 + 7 = 139 + 5x must be divisible by 11. 

The only value of x as a digit the satisfies above is 3. With that, total sum 154 is divisible by 11.

Hence, the account number must be, 317034847. 

 

Breaking The Safe in 5 Minutes?

Charlie Croker and his team need to break the safe to finish a secret job named "Italian Job" in exactly a five minutes.

They got just one chance and five minutes to finish the job else the local police will be informed.

He got following clues

1st Clue: Exactly one number is perfectly placed.
9 2 5

2nd clue: Everything is incorrect.
9 3 8

3rd clue: Two numbers are part of the code of the safe, but are wrongly placed.
4 9 6

4th clue: One number is part of the code of the safe, but is wrongly placed.
5 8 1

5th clue: One number is part of the code of the safe, but is wrongly placed.
1 2 6 

This should be the process!

To Break The Safe in 5 Minutes...

What was the challenge? 

Re listing all the clues...

1st Clue: Exactly one number is perfectly placed.
9 2 5

2nd clue: Everything is incorrect.
9 3 8

3rd clue: Two numbers are part of the code of the safe, but are wrongly placed.
4 9 6

4th clue: One number is part of the code of the safe, but is wrongly placed.
5 8 1

5th clue: One number is part of the code of the safe, but is wrongly placed.
1 2 6 

------------------------------------------------------------------------------------------------

From 2nd clue, it's clear that 9,3,8 are not part of the code.

Hence correct number suggested by 1st clue must be 2 or 5

Since 9 is not part of the code, the other 2 correct numbers that 3rd clue pointing must be 4 and 6.

If 6 is the part of code, then 1 & 2 are not as 5th clue is suggesting.

And since 2 isn't part of the code then 1st clue must be pointing 5 is correct digit placed in right position.

The 4th clue is also suggesting that 5 is the part of the code but not 1 or 8.

If 5 is correct at it's position as per first clue then 4 and 6 must be occupying other 2 places.

As per 3rd clue position of 4 is wrong, it must be at second place and hence 6 at first place.

Hence the code is 645!

A Railway And Cyclist Crossing

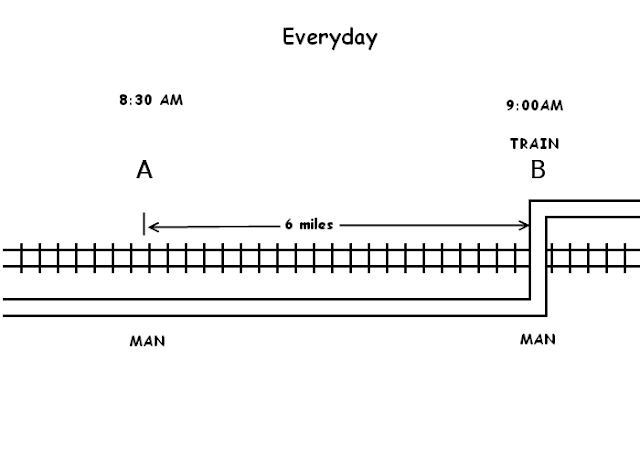
A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. 

What was the speed of the train?

Skip To Know The Speed Of The Train! 

To Cross The Cyclist...

What was the scenario?

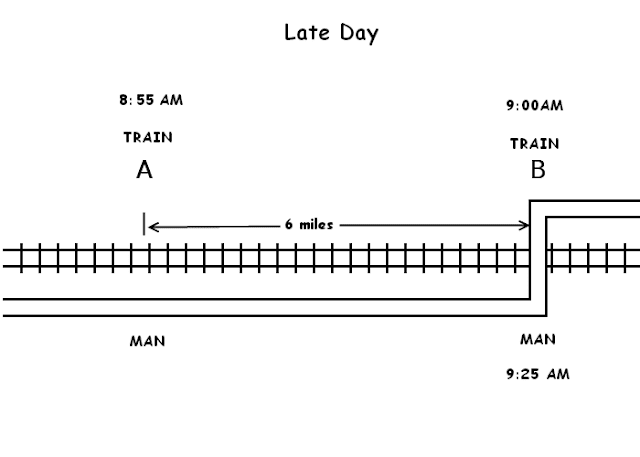
 Let's suppose he reaches the crossing at 9:00 AM. Usually at 8:30 AM he is at point A, 6 miles before the usual crossing point B (speed of 12 mph, means 6 mile per half hour).

On the day on which he was late by 25 minutes, he must be again at point A (i.e. 6 miles ahead of usual crossing point B) at 8:55 AM. So at this point, both train and man were at the same point A. And the train as everyday, reaches point B at 9:00 AM. That means, it travels 6 miles in 5 minutes. Hence, train must be traveling at 72 mph.