Skip to main content
Posts
What was the puzzle?
Let's recollect the given clues once again.
- There are five houses in a row. Each of the houses is painted a
different color, and their occupants come from different countries, own
different pets, drink different beverages, and smoke different cigarette
brands.
- The Englishman lives in the red house.
- The Spaniard owns the dog.
- Coffee is drunk in the green house.
- The Ukrainian drinks tea.
- The green house is immediately to the right (your right) of the ivory house.
- The Old Gold smoker owns snails.
- Kools are smoked in the yellow house.
- Milk is drunk in the middle house.
- The Norwegian lives in the first house.
- The man who smokes Chesterfields lives in the house next to the man with the fox.
- Kools are smoked in the house next to the house where the horse is kept.
- The Lucky Strike smoker drinks orange juice.
- The Japanese smokes Parliaments.
- The Norwegian lives next to the blue house.
================================================================
STEP 1 :
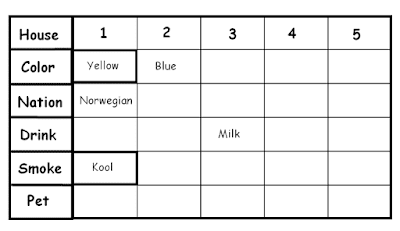
As per clue (1), let's create a table like below, and then fill the data one by one.
================================================================
STEP 2 :
As per clue (9),(10) and (15),
================================================================
STEP 3 :
As per (2), Englishman lives in red house, that means it can't be first house. Also, (6) points that green house is next to ivory. So, ivory-green can't be at 1-2 positions. But those can be at 3-4 with red at 5 or at 4-5 with red at 3.
In short, only color left for 1 is yellow. And as per (8), Kools are smoked in the yellow house.
=================================================================
STEP 4 :
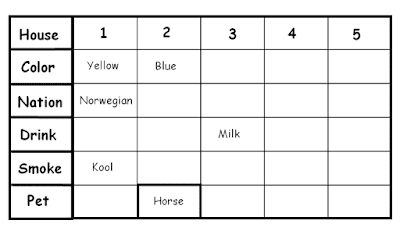
Now as per (12), Kools are smoked in the house next to the house where the horse is kept.
=================================================================
STEP 5 :
Let's assume the red house of Englishman is at no.5 then Ivory-Green are at no.3-4.
Since as per (4), green house owner drinks coffee, and only position left for Ukrainian drinking tea pointed by (5) is house no.2.
=================================================================
STEP 6 :
Now the luck strike smoker drinking orange juice pointed by (13) has only position and that is house no.5. That leaves only drink available for house 1 as water.
As per (3), Spaniard who owns dog has houses 3 and 4 available but for Old Gold smoker (pointed by (7)) also available houses are 3 and 4 again.
If Old Gold smoker occupies house 3 then Spaniard who own dog would have house 4. In that case, there will be no position would be left for Japanese smoking Parliaments (Clue no.14).
Same can be proved if Old Gold smoker occupies house no.4.
Hence, our assumption made in step 5 is wrong. So, Red house must be at 3 owned by Englishman.
===============================================================
STEP 7 :
So if Englishman's red house is at no.3 then at no.4 & 5 there must be ivory and green houses where coffee is drink in green house.
================================================================
STEP 8 :
Now, for Lucky Strike smoker who drinks orange juice (clue 13) and Ukrainian who drinks tea (clue 5) only available houses are (see above table) house no.2 & 4. That is, 2 and 4 are occupied by tea & orange juice drinkers (order yet unknown). With that, we can conclude that the drink in first house is Water.
==============================================================
STEP 9 :
If we assume that Lucky Striker smoker who drinks Orange juice (clue 13) live in house no.2 then Ukrainian who drinks tea (clue 5) has to be in house no.4. With that, Japanese who smokes Parliament (clue 14) need to be in the house no.5. No house is left for Spaniard who owns the dog (clue 3) as house no.2 is already occupied by pet horse.
That's why the Lucky Strike smoker with Orange juice as drink must be in house no.4.
================================================================
STEP 10 :
Now, if Lucky Strike smoker (clue 13) is living in house no.4 then Ukrainian who drinks tea (clue 5) must be in house no.2. With that, Japanese who smokes Parliament (clue 15) needs to be in house no.5 and Spaniard who owns dog (clue 3) needs to be in house no.4.
===============================================================
STEP 11 :
In the end, for Old Gold smoker (clue 7) only house left is house no.3. And as per clue 11,Chasterfield smoker needs to be in the house followed by fox owner. Hence, they must be in the house no.1 and 2 respectively. Finally, the only pet left for house no.5 is Zebra.
==============================================================
CONCLUSION :
The final table looks like -
Now, finding answers of given questions is easy from the table.
Who drinks water?
- Norwegion
Who owns the zebra?
- Japanese
A rower rows regularly on a river, from A to B and back. He’s got into
the habit of rowing harder when going upstream, so that he goes twice as
fast relative to the water as when rowing downstream.
One day as he’s
rowing upstream he passes a floating bottle. He ignores it at first but
then gradually grows curious about its contents. After 20 minutes of
arguing with himself he stops rowing and drifts for 15 minutes. Then he
sets out after the bottle. After some time rowing downstream he changes
his mind, turns around, and makes his way upstream again. But his
curiosity takes hold once more, and after 10 minutes of rowing upstream
he turns and goes after the bottle again. Again he grows ashamed of his
childishness and turns around. But after rowing upstream for 5 minutes
he can’t stand it any longer, rows downstream, and picks up the bottle 1
kilometer from the point where he’d passed it.
How fast is the current?
That's the speed of water current!
What was the story?
Just for a moment let's assume the rower is rowing on a calm lake where water is stationary. Then, the bottle that he saw is also not moving & floating at one point.
In the case, he moves away (upstream in real case) from the bottle & comes back (downstream in real case) again to collect the bottle. He rows away from the bottle for 20 + 10 + 5 = 35 minutes.
Remember his speed is double when he goes away from bottle than when he is coming towards the bottle. That's why he takes 35 X 2 = 70 minutes to come back at the point where bottle is floating.
Moreover, he drifts for 15 minutes in real case; for that let's assume he sits motionless for 15 minutes (in our assumed lake case) at some point in between.
So after leaving the bottle, he returns to the bottle after 35 + 15 + 70 = 120 minutes.
Now, assume this water in the lake is moving and this bottle is 'displaced' by 1 KM away from it's original position in 120 minutes.
That means, the water is moving at the speed of 1 km / 120 minutes. That is the speed of water current is 1/2 kmph.
You and I have to travel from Startville to Endville, but we have
only one bicycle between us. So we decide to leapfrog: We’ll leave
Startville at the same time, you walking and I riding. I’ll ride for 1
mile, and then I’ll leave the bicycle at the side of the road and
continue on foot. When you reach the bicycle you’ll ride it for 1 mile,
passing me at some point, then leave the bicycle and continue walking. And
so on — we’ll continue in this way until we’ve both reached the
destination.
Will this save any time?
You say yes: Each of us is riding for part
of the distance, and riding is faster than walking, so using the bike
must increase our average speed.
I say no: One or the other of us is always walking; ultimately every
inch of the distance between Startville and Endville is traversed by
someone on foot. So the total time is unchanged — leapfrogging with the
bike is no better than walking the whole distance on foot.
Who’s right?
Look who is right in the case!
Where I went wrong?
That's going to save time for sure.
Let's assume that the distance between Startville and Endville is 2 miles. And suppose we walk at the same speed of 4 mph and ride bicycle at the speed of 12 mph.
Then I will travel for first 1 mile in 5 minutes leave the bicycle and start walking thereafter. You take 15 minutes to reach at the point to pick up bicycle and ride next mile. For next mile, I need 15 minutes as I am walking & you need only 5 minutes ride on bicycle. So exactly after 20 minutes we will reach at Endville.
And what if we had walked entire 2 miles distance? It would have taken 30 minutes for us to reach at the destination.
One thing you must have noticed, each of us walked for 1 mile only and ride on bicycle for other mile which saved 10 minutes of our journey. Imagine it as if we had 2 bicycles where we ride 1 mile in 5 minutes, leave bicycles and walk next mile in another 15 minutes.
So my argument in the case is totally wrong. It would have been correct if I had waited for you after finishing 1 mile ride on bicycle and then started to walk next mile.
In that case, you will reach at the destination in 20 minutes but I need 30 minutes as I wasted 10 minutes in middle.
Conclusion:
My argument -
"One or the other of us is always walking; ultimately every inch of the
distance between Startville and Endville is traversed by someone on
foot."
tells only half story.
Yes, ultimately every inch of the
distance between Startville and Endville is traversed by someone on
foot but the distance that each of us walk is equal though different parts of journey. And for the rest of distance we ride on bicycle where total time required for journey is saved.
200 students are arranged in 10 rows of 20 children. The
shortest student in each column is identified, and the tallest of these
is marked A. The tallest student in each row is identified, and the
shortest of these is marked B. If A and B are different people, which is
taller?
This person will be taller in any case!
Why the height comparison?
B will be always taller in any case.
Case 1 : If A and B are standing in the same row the obviously B is taller than A as B is tallest among all in that row.
Case 2 : If A and B are standing in the same column then still B is taller than A as A is shortest among all in that column.
Case 3 : If A and B are standing in different row and column then there must be somebody C which has same column as A and same row as B. This C is shorter than B (as B is tallest in row) and he is taller than A (as A is shortest in that column). That is B > C and C > A.
Hence, in any case, B is always taller than A.
Marissa and Juliana went out for drinks together. They ordered the same
drink. Juliana was really thirsty and finished five in the time it took
Marissa to finish one. The drinks were poisoned, but only Marissa died.
How?
TIP : Poison wasn't in Marrisa's glass neither added externally by any one.
This is how Juliana survived!
What was the incident?
That's because the poison was in the ice. Since Marissa took time to drink her first, the ice melted & poison got mixed up in the drink very well. Whereas, Juliana was thirsty & finished drinks in hurry; it didn't get enough time to melt the ice & hence poison didn't get mixed up with the drink. That's how Juliana survived!
A fair die bearing the numbers 1, 2, 3, 4, 5, 6 is repeatedly thrown
until the running total first exceeds 12. What’s the most likely total
that will be obtained?
This must be the most likely total!
Here is the question!
Just consider the the next-to-last throw where last throw would make total exceeding 12.
Till then total must be either of 12,11,10,9,8 or 7. And next throw will make total greater than 12.
At this point -
If total is 12 then the first total exceeding 12 could be any from 13,14,15,16,17,18.
If total is 11 then the first total exceeding 12 could be any from 12,13,14,15,16,17,
If total is 10 then the first total exceeding 12 could be any from 12,13,14,15,16.
If total is 9 then the first total exceeding 12 could be any from 12,13,14,15.
If total is 8 then the first total exceeding 12 could be any from 12,13,14.
If total is 7 then the first total exceeding 12 could be any from 12,13.
It's quite evident that the number 13 appears in every above case.
Hence, 13 is the most likely total.
A man stuck in a small sailboat on a perfectly calm lake throws a stone overboard. It sinks to the bottom of the lake.
When the water again settles to a perfect calm, is the water level in the lake higher, lower, or in the same place compared to where it was before the stone was cast in?
Did you think it will rise?
But why water level was affected?
Do you recall what does Archimedes Principle state? For an object to float on water, it has to displace that much volume of water whose weight is equal to weight of the object itself. Now if object has less density than water then obviously it has to displace lesser amount of volume of water to float on it. That means it has to sink less in water.
For a moment, let's assume the stone has very high density & hence having weight equal to hundreds of kilograms despite of having small volume.
Here, stone sinks to the bottom of the lake suggests that it is has more density than water. It can't displace the water whose weight is equal to it's weight.But when it was on sailboat it could push the sailboat down so that more water is displaced weighing equal to it's weight. Result of this, the sailboat sinks little 'deeper' compared to when stone wasn't there.
Obviously, the volume of displaced water when stone was in sailboat (due to stone only) must be greater that the volume of displaced water when stone sinks to the bottom of the lake. That's why both sailboat and stone together could float on the water. In short, sailboat helped stone to displace amount of water needed to float which results in rise in shoreline.
And when stone is thrown out of the sailboat, then ideally it can't displace more water than when it was on sailboat. Now, sailboat sinks less 'deeper' in water displacing only water need to float itself.

That's why the water level must be dropped compared to earlier. The little rise due to water displaced by stone can't exceed the earlier water level for the reason explained above.
A square tabletop measures 3n × 3n. Each unit square
is either red or blue. Each red square that doesn’t lie at the edge of
the table has exactly five blue squares among its eight neighbors. Each
blue square that doesn’t lie at the edge of the table has exactly four
red squares among its eight neighbors. How many squares of each color
make up the tabletop?
Here is correct way to count those!
How squares are arranged?
The tabletop measures 3n × 3n, so we can divide it evenly into n2 ( 3 × 3) squares that together tile the surface completely.
Let's consider a piece of square of size 3 x 3. For each such unit of 3 x 3 -
1. If the center of the square is red square, then there are 5 blue squares and 3 red squares surrounded with it.
2. If the center is blue square, then there are 4 blue and 4 red squares surrounding that square.
In any case, for 3 x 3 = 9 squares, there are 5 blue and 4 red squares.
Therefore, for tabletop of 3n x 3n, there will be 5n2 blue squares and 4n2 red squares.
One fine day, Mr. Puzzle and Mr. Fry were playing cards, but suddenly
power went off and they were getting bored. So Mr. Puzzle randomly
inverted position of 15 cards out of 52 cards(and shuffled it) and asked
Mr. Fry to divide the card in two pile with equal number of inverted
cards (number of cards in each pile need not be equal).
It was very dark in the room and Mr. Fry could not see the cards,
after thinking a bit Mr. Fry divided the cards in two piles and quite
surprisingly on counting number of inverted cards in both the piles were
equal.
What do you think Mr. Fry must have done?
This is what he must have done!
What was the challenge?
Mr.Fry must have taken top 15 cards & inverted positions of all. So he divides deck into 2 piles - one with 15 cards & other 37 cards.
Now suppose if there are 7 cards that were inverted in top 15 & 8 were inverted in remaining 37. When he flips top 15, 7 remains in normal position & 8 remains in inverted position. That is equal to 8 cards in inverted position from pile of 37 cards.
In short, if there are N cards inverted in top 15 then there are 15 - N cards inverted in remaining 37 cards. So on flipping position of top 15, there will be 15 - N cards in inverted position in top 15. That's how both piles would have equal number of inverted cards i.e. 15-N.
Had Mr.Puzzle inverted positions of 20 cards randomly then Mr. Fry would have flipped top 20 cards. He would have made 2 piles with one with 20 cards & other 32 cards to equate the count of inverted cards in piles.
Three robbers, Babylas, Hilary, and Sosthenes, are stealing a
treasure chest from the top of an old tower. Unfortunately, they’ve had
to destroy their ladder to avoid pursuit, so they’ll have to descend
using a crude tackle — a single pulley and a long rope with a basket at
each end.
Babylas weighs 170 pounds, Hilary 100 pounds, Sosthenes
80 pounds, and the treasure 60 pounds. If the difference in weight
between the two baskets is greater than 20 pounds then the heavier
basket will descend too quickly and injure its occupant (though the
treasure chest can withstand this).
How can the three of them safely
escape the tower with the treasure?
That's how they escape!
What was the challenge in escaping the tower?
Note that difference between weights in 2 baskets can't exceed 20 pounds. However, chest can withstand the shock even if the difference exceeds that limit
1.
They put 60 pounds chest in one of empty basket & sends it down. (60 pounds vs 0 Pounds)
2. Sosthenes of 80 pounds climbs in other empty basket and rides down to the ground while bringing up the chest. (60 pounds vs 80 pounds)
3. Now chest is taken out and Hilary is sent down while bringing up Sosthenes.(80 pounds vs 100 pounds).
4. Hilary gets out of the basket on ground and Sosthenes get out of the basket at top of the tower.
5. They again send chest of 60 pound to the ground putting it in 1 basket. This brings other empty basket up at the top of the tower.
6. Now, Hilary (who is on ground) climbs in the basket with chest (total weight = 60 + 100 = 160 pounds) while Babylas (170 pounds) enters in the basket at the top of tower. This allows Babylas to ride down to the ground. (160 pounds vs 170 pounds).
Right now, Babylas is on ground and Hilary, Sosthenes are on the top of the tower with chest.
7. Here, Babylas jumps on the ground & Hilary gets out of the basket at the top of tower.
8. Again, because of chest which weighs 60 pounds the basket descends down to the ground bringing up other basket up. (60 pounds vs 0 Pounds).
9. Now, Sosthenes (at top) rides down to the ground bringing up the chest. (60 pounds vs 80 Pounds).
10. Hilary replaces himself with the chest at the top and rides down while bringing Sosthenes up. (100 pounds vs 80 Pounds).
At the moment, Sosthenes is at the top with chest while Hilary and Babylas are on the ground.
11. Now, Sosthenes sends back chest on the ground & then rides to the ground while entering into other empty basket. (60 pounds vs 80 Pounds).
12. And when Sosthenes gets out of the basket on the ground the basket with chest descends on it's own to the ground.
13. Finally, all Sosthenes, Babylas and Hilary take chest out of the basket and safely escape the tower.