Skip to main content
Posts
What was the situation?
Let's first have statements by 2 creatures -
A: B is a lying monkey. I am human.
B: A is telling the truth.
If we assume B is telling the truth then A is also telling the truth. But A in statement says B is lying which contradicts our assumption.
Hence, B must be lying. If B is lying then statement of B suggest that A is also must be lying. That mean 'B is lying monkey' part of statement made by A is too lie. Since we have deduced already B is lying, the lying statement of A suggests that B is not monkey. Hence B is the lying man!
Other lie spoken by A is that it is human. Hence A must be a lying monkey!
Today, John has to transfer 50 euro to the bank account of a Dutch
friend. He has written down the account number on a piece paper. But
since he had forgotten to take out the paper from his trousers when he
put them in the washing machine, one digit of the bank account number
became unreadable. The note says: 3170?4847.
The friend of John is
climbing the Mount Everest at the moment, so it is impossible for John
to call his friend. Suddenly he remembers that a for a valid Dutch bank
account number it holds that the first digit times 9 + the second digit
times 8 + the third digit times 7 + ...... + the ninth digit times 1
should be divisible by 11. John thinks for a moment and finds the
correct number.
What is it?
That it is !
What were the clues?
Let x be that missing digit. Then the bank account number looks like, 3170x4847.
Now 9 x First Digit + 8 x Second Digit + 7 x Third Digit.......must be divisible by 11.
That is 27 + 8 + 49 + 0 + 5x + 16 + 24 + 8 + 7 = 139 + 5x must be divisible by 11.
The only value of x as a digit the satisfies above is 3. With that, total sum 154 is divisible by 11.
Hence, the account number must be, 317034847.
Charlie Croker and his team need to break the safe to finish a secret job named "Italian Job" in exactly a five minutes.
They got just one chance and five minutes to finish the job else the local police will be informed.
He got following clues
1st Clue: Exactly one number is perfectly placed.
9 2 5
2nd clue: Everything is incorrect.
9 3 8
3rd clue: Two numbers are part of the code of the safe, but are wrongly placed.
4 9 6
4th clue: One number is part of the code of the safe, but is wrongly placed.
5 8 1
5th clue: One number is part of the code of the safe, but is wrongly placed.
1 2 6
This should be the process!
What was the challenge?
Re listing all the clues...
1st Clue: Exactly one number is perfectly placed.
9 2 5
2nd clue: Everything is incorrect.
9 3 8
3rd clue: Two numbers are part of the code of the safe, but are wrongly placed.
4 9 6
4th clue: One number is part of the code of the safe, but is wrongly placed.
5 8 1
5th clue: One number is part of the code of the safe, but is wrongly placed.
1 2 6
------------------------------------------------------------------------------------------------
From 2nd clue, it's clear that 9,3,8 are not part of the code.
Hence correct number suggested by 1st clue must be 2 or 5
Since 9 is not part of the code, the other 2 correct numbers that 3rd clue pointing must be 4 and 6.
If 6 is the part of code, then 1 & 2 are not as 5th clue is suggesting.
And since 2 isn't part of the code then 1st clue must be pointing 5 is correct digit placed in right position.
The 4th clue is also suggesting that 5 is the part of the code but not 1 or 8.
If 5 is correct at it's position as per first clue then 4 and 6 must be occupying other 2 places.
As per 3rd clue position of 4 is wrong, it must be at second place and hence 6 at first place.
Hence the code is 645!
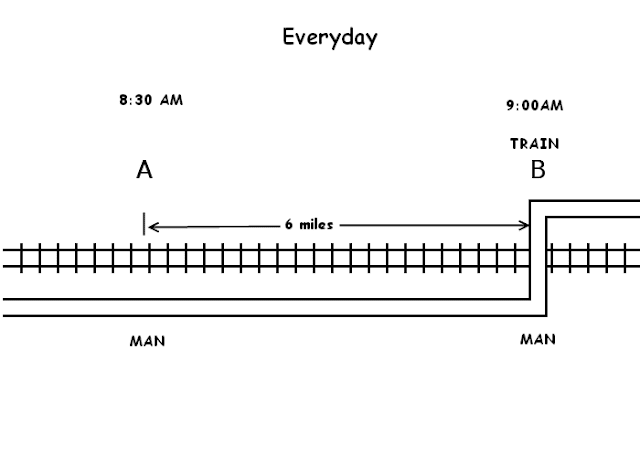
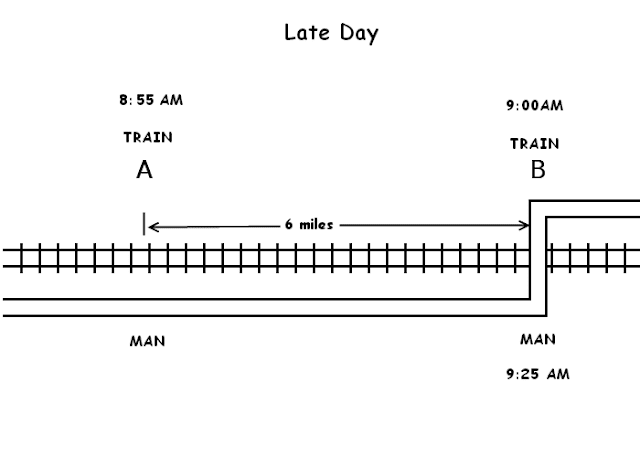
A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing.
What was the speed of the train?
Skip To Know The Speed Of The Train!
What was the scenario?
Let's suppose he reaches the crossing at 9:00 AM. Usually at 8:30 AM he is at point A, 6 miles before the usual crossing point B (speed of 12 mph, means 6 mile per half hour).
On the day on which he was late by 25 minutes, he must be again at point A (i.e. 6 miles ahead of usual crossing point B) at 8:55 AM. So at this point, both train and man were at the same point A. And the train as everyday, reaches point B at 9:00 AM. That means, it travels 6 miles in 5 minutes. Hence, train must be traveling at 72 mph.