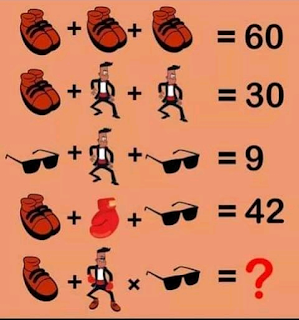Skip to main content
Posts
How the master was challenged?
Let's assume once again A, B and C are those logicians and C has guessed the color of own hat correctly. Here is what he must have thought -
============================================================================
"I'm assuming the grand master is conducting this test fairly denying any sort of advantage to any participant.
With that assumption, the grand master can't put 2 white and 1 black hat on heads. In that case, the person having black hat and watching 2 white hats on others' head would know the color of own hat immediately.
For fair play, he can't put 2 blacks and 1 white hat either. That will give unfair advantage to the logicians wearing black hats. Suppose A and B are wearing black and I'm wearing white hat. Now, what A (or B) would be thinking -
---------------------------------------------------------------------------------------------------
" I'm A (or B) and I can see 1 black and 1 white hat (on head of C). If I have white
hat on my head then B (or A) would know color of his hat as black as there are
only 2 white hats available and those would be on my head and C's head.
Moreover, 1 black and 2 white hats already eliminated as it's unfair distribution.
That means I must be wearing black hat."
---------------------------------------------------------------------------------------------------
That's how the combination of 2 black and 1 white hats also eliminated from fair play.
Hence, all of three must be wearing black hats is only fair distribution giving all of us equal chance of winning and hence I must be wearing black hat only.
============================================================================
Note : Here, C is assumed as a winner for only sake of convenience, otherwise either A or B whoever is wisest can be winner.
Three Masters of Logic wanted to find out who was the
wisest among them. So they turned to their Grand Master, asking to
resolve their dispute.
"Easy," the old sage said. "I will blindfold you and paint
either red, or blue dot on each man's forehead. When I take your
blindfolds off, if you see at least one red dot, raise your hand. The
one, who guesses the color of the dot on his forehead first, wins."
And so it was said, and so it was done.
The Grand Master
blindfolded the three contestants and painted red dots on every one.
When he took their blindfolds off, all three men raised their hands as
the rules required, and sat in silence pondering.
Finally, one of them
said: "I have a red dot on my forehead."
How did he guess?
And this is how his logical brain responded!
Similar kind of puzzles are -
The Greek Philosophers
Real Test Of Genius
What was the test?
Let A, B and C be the names of three logicians and C be the logician who correctly guessed the color of dot on forehead.
Now, this could be the C's logic behind his correct guess -
"If I had blue dot on my forehead then A and B must had raised hands after looking red dots on the foreheads of other. In case, what A (or B) would have thought? His logic would be -
"If C is with the blue dot then B (or A) must have raised hand after noticing
red dot on my forehead, hence I must have red dot."
So A (or B) would have successfully guessed color of dot on own forehead easily.
But neither A or B not responding that means I must have red dot on my forehead!"
The logician who guess it correctly could be either A or B not necessarily be C; here it is assumed C is wisest for the sake of convenience.
What was the equation?
From picture, it is clear that,
Pair of shoes = 20, single shoe = 10
Man = 5
Goggles = 2
Single Glove = 20
Now, equation in question has man with 2 shoes, 2 gloves and 1 goggles hence his value in equation = 20 + 40 + 5 + 2 = 67
Hence, final equation appears as
10 + 67 x 2 = 144.
The answer is 144.
We have two white, two red and two blue balls. For each color, one ball
is heavy and the other is light. All heavy balls weigh the same. All
light balls weigh the same. How many weighing on a beam balance are
necessary to identify the three heavy balls?
You need only 2 weighings! Click here to know how!
What was the task given?
Actually, we need only 2 weighing.
Weigh 1 red & 1 white ball against 1 blue & 1 white ball. Weighing result between these balls helps us to deduce the relative weights of other balls.
----------------------------------------------------------------------------------------------------
Case 1 :
If this weighing is equal then the weight of red ball and blue ball are different.
That's because the weighing is equal only when there is combination of
H (Heavy) + L (Light) against L (Light) + H (Heavy).
Since, one white ball must be heavier than the other white ball placed in other pan, the red & blue balls place along with them must be of 'opposite' weights with respect to the white balls place along with them.
So weigh this red against blue will give us the heavier red (or blue) leaving other red (or blue) as lighter.
If red (or blue) weighs more in this weighing then the white ball placed with this red (or blue) in first weighing must be lighter than the other white ball placed with blue (or red) ball.
----------------------------------------------------------------------------------------------------
Case 2 : Red + White > Blue + White.
The white ball in Red + White must be heavier than the white ball in Blue + White.
The reason is if this white was lighter then even heavier red in the Red + White can't weigh more than Blue + White having heavier white. That is H + L can't beat H + H or obviously would equal with H + L!
So we have got the heavier and lighter white balls for sure.
Now, weigh red from Red + White and blue from Blue + White against other red and blue balls left.
Case 2.1/2.2 : Red + Blue > or < Red + Blue
Obviously, red and blue balls in left pan are heavier (or lighter) than those in other.
------------------------------------------------------------------------------------
Case 2.3 : Red + Blue = Red + Blue
Obviously, that's because of H + L = L + H.
But the red is taken from Red + White which was heavier than the Blue + White.
Since, L + H (white is heavier as concluded) can't weigh more than H + L
(other white is lighter as concluded) or L + L, the red in Red + White
must be heavier making H + H combination in that pan in first weighing (case 2).
So, we got heavier red and lighter blue obviously leaving lighter red
and heavier blue in other pan.
----------------------------------------------------------------------------------------------------
Case 3 : Red + White < Blue + White.
Just replace Red with blue & vice versa in the deduction made in case 2.
----------------------------------------------------------------------------------------------------