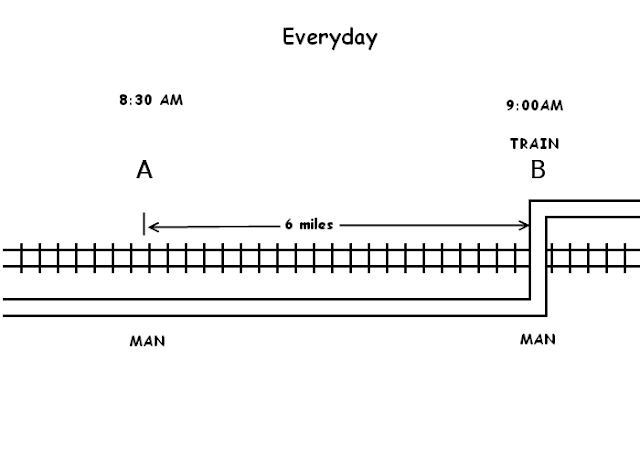
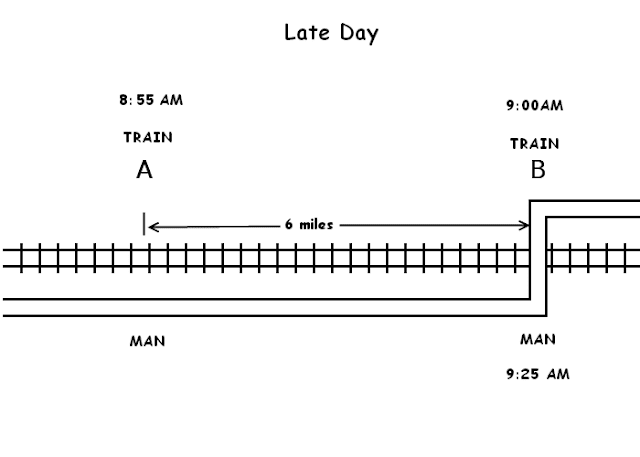
Cars Around Interesting Circular Track

Around a circular race track are n race cars, each at a different location. At a signal, each car chooses a direction and begins to drive at a constant speed that will take it around the course in 1 hour. When two cars meet, both reverse direction without loss of speed. Show that at some future moment all the cars will be at their original positions.

Here is that proof!


Source 

Analysing Interesting Circular Race Track

What was the interesting fact about?

Just imagine that each car carries a flag on it and on meeting pass on that flag to the next car. Obviously, this flag will move at the constant speed around the track as cars carrying it are also moving at the constant speed. So, the flag will be back at the original position after 1 hour.

Let's assume there are only 2 cars on the track at diagonally opposite points as shown below. 

After 15 minutes, on meeting with Car 2, Car 1 will pass on the flag & both will reverse their own direction. 30 minutes later (i.e. 45 minutes after start) both cars again meet each other and Car 2 will pass on flag back to Car 1 & directions are reversed again. Again in another 15 minutes (i.e. after 1 hour from start), both cars are back at the original positions. 

Now, let's suppose that there are 4 cars on the track positioned as below.

The above image shows how cars will be positioned after different points of time & how they reverse direction after meeting.

Again, all are back to the original position after 1 hour including the flag position. One more thing to note that the orders in which cars are never changes. It remains as 1-2-3-4 clockwise. 

To conclude, for 'n' number of cars, at some point of time all the cars will be in original positions in future.   
 

A Railway And Cyclist Crossing

A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. 

What was the speed of the train?

Skip To Know The Speed Of The Train! 

To Cross The Cyclist...

What was the scenario?

 Let's suppose he reaches the crossing at 9:00 AM. Usually at 8:30 AM he is at point A, 6 miles before the usual crossing point B (speed of 12 mph, means 6 mile per half hour).

On the day on which he was late by 25 minutes, he must be again at point A (i.e. 6 miles ahead of usual crossing point B) at 8:55 AM. So at this point, both train and man were at the same point A. And the train as everyday, reaches point B at 9:00 AM. That means, it travels 6 miles in 5 minutes. Hence, train must be traveling at 72 mph.  

The Dog Of The Commander

A long and straight row of soldiers is marching with constant speed. The dog of the commander runs along the row from the end till the beginning, from the beginning till the end, from the end till the beginning etc. This takes always 2 minutes, 1 minute, 2 minutes, etc. 

At some point the soldiers have to pass a very small bridge. However, the commander does not trust the strength bridge completely. He wonders how much time it will take them to pass the bridge when they stay marching with the same speed. 

How much time is that?  

You can skip to the answer! 

Passing A Very Small Bridge

What is the question?

For march of soldiers to pass any point, there must be first man crossing that point first and then later the last man should cross the same point. 

Now the dog runs from the first to last man in 1 minute, then runs back to first man in 2 minutes and again back to last man in 1 minutes. That means the dog must be at the same point where he started journey from first man. In other words, the dog has run for 2 minutes in both the directions. Hence, he must be at the same point after 4 minutes.

Interestingly, the dog was at first man when started & after 4 minutes ended at the last man of the march. Since dog is at the same point after 4 minutes, the entire march of soldiers is crossed that point in 4 minutes as first and last man have crossed that point.

The same when applied to a very small bridge which can be assumed as a point, we can say that it requires 4 minutes for soldiers to cross it.
 

Complex Time, Speed & Distance Maths

There is a circular race-track of diameter 1 km. Two cars A and B are standing on the track diametrically opposite to each other. They are both facing in the clockwise direction. At t=0, both cars start moving at a constant acceleration of 0.1 m/s/s (initial velocity zero). Since both of them are moving at same speed and acceleration and clockwise direction, they will always remain diametrically opposite to each other throughout their motion.

At the center of the race-track there is a bug. At t=0, the bug starts to fly towards car A. When it reaches car A, it turn around and starts moving towards car B. When it reaches B, it again turns back and starts moving towards car A. It keeps repeating the entire cycle. The speed of the bug is 1 m/s throughout.

After 1 hour, all 3 bodies stop moving. What is the total distance traveled by the bug?

Find out complex calculations here!

Simple Solution of Complex Problem

Here is that complex looking problem! 

Everything built, written or designed in the given problem is to distract you from basic physics formula.

Speed = Distance / Time

Hence,

Distance = Speed x Time 

All the details given except speed of bug & time for which it traveled are there to confuse you. Speed of bug is 1 m/s & it traveled for 1 hour = 3600 seconds.

Distance = 1 x 3600 = 3600 m

So the total distance traveled by the bug is 3600 m.