Sara's Desert Trek
Sara needs to trek from an oasis to a destination 10 miles away across a barren desert.
The facts:
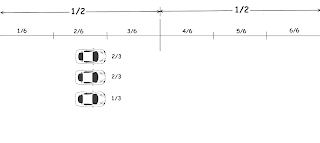
This is how she optimizes her journey!
The facts:
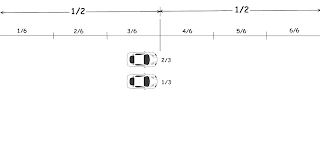
- Crossing one mile of desert requires using 1 gallon of water.
- Sara can only carry 6 gallons of water at a time.
- Sara can drop a water cache (of any amount of water from the supply she is carrying at that moment) at any of the nine stops along the route, and then pick up any part of the cache on a later trip.
This is how she optimizes her journey!