The Love Island

Four men and four women are in Love Island. Each one falls in love with another and is himself/herself loved by someone else in a complete 8 person loop.

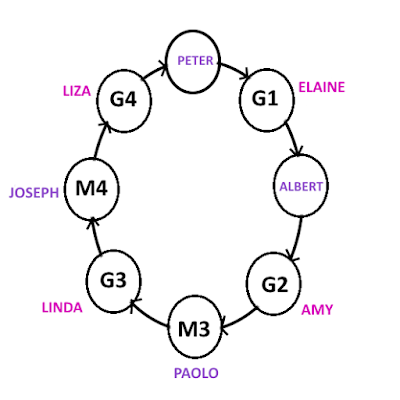
Peter falls in love with a girl who is unfortunately in love with Albert. Joseph loves a girl who loves the man who loves Elaine. Liza is loved by the guy who is loved by the girl who is loved by Paolo. Linda hates Paolo and is hated by the man whom Amy loves.

No guy/guy or girl/girl in Love Island.

Who loves Joseph and whom does Joseph love?

Know here who loves Joseph and Joseph loves whom! 

The Love Loop on the Love Isaland

What was the puzzle?

There are few hints given in the question.

-----------------------------------------------------------


1. Peter falls in love with a girl who is unfortunately in love with Albert. 

2. Joseph loves a girl who loves the man who loves Elaine. 

3. Liza is loved by the guy who is loved by the girl who is loved by Paolo. 

4. Linda hates Paolo and is hated by the man whom Amy loves.

----------------------------------------------------------- 

STEPS :

STEP 1 :

Let's name all 4 men as M1, M2, M3 and M4 while girls as G1, G2, G3 and G4.

STEP 2 :

Let's start with Peter. He can be at any position M1, M2, M3 or M4. Let's assume that he is at M1. As (1) points M2 must be Albert.

STEP 3 :

As per (2), there are 2 persons in between Joseph and Elaine. That is Joseph can be at M3 or M4 while Elaine can be at G4 or G1 respectively. Exactly, same are possible locations for Paolo and Liza respectively in the loop as (3) suggests.

STEP 4 :

In short, at M3 and M4, we have Joseph and Paolo and G1, G4 are occupied by Liza and Elaine but exact location yet to be known.

STEP 5 :

For The statement (4) to be TRUE, Linda must be hating Paolo. 

 👉 CASE 5.1 : If Paolo is at M3 then Linda can't be at G2 hence must be at G3. With that, Joseph will be at M4, Elaine at G1, Liza at G4 & only location for Amy as G2.

 👉 CASE 5.2 : If Paolo is at M4 then Linda can't be at G3 hence must be at G2. With that, Joseph will be at M3, Elaine at G4, Liza at G1 & only location for Amy as G3.

CASE 5.1 make other part of the statement (4) false i.e. Linda is hated by man (Paolo here) whom Amy loves is false in the case.

Hence, CASE 5.2 is valid and the final loop looks as - 

Finally, turning to the question asked.

Q. Who loves Joseph and whom does Joseph love?

A. Linda loves Joseph and Joseph loves Amy.

Crucial Support of a Girlfriend - Puzzle

A man escapes from jail with help from his girlfriend. Four girls are accused of being the man's girlfriend. His girlfriend is lying. Two girls are innocent and telling the truth. The other girl is the man's sister who is helping the girlfriend lie. 

Who is the man's sister?

Amanda: "Melinda is his girlfriend."

Vanessa: "Eva is lying."

Eva: "Amanda is lying."

Melinda: "Vanessa is not his sister."

Know who is man's sister! 

Crucial Support of Girlfriend Puzzle : Solution

What was the puzzle?

What we know so far.

A man escapes from jail with help from his girlfriend. Four girls are accused of being the man's girlfriend. His girlfriend is lying. Two girls are innocent and telling the truth. The other girl is the man's sister who is helping the girlfriend lie. 

And statements of four girls are - 

Amanda: "Melinda is his girlfriend."

Vanessa: "Eva is lying."

Eva: "Amanda is lying."

Melinda: "Vanessa is not his sister."

Now, for a moment, let's assume Amanda is telling the truth. Then Melinda must be man's girlfriend who is lying. Therefore, Vanessa must be man's sister who is lying in support of man's girlfriend Melinda. 

So, Vanessa's lying statement suggests that Eva must be telling the truth. But as per Eva, Amanda is lying which is contrary to our initial assumption that Amanda is telling the truth.

So, Amanda must be lying.

If Amanda is lying then Eva must be telling the truth. And if Eva is telling the truth then Vanessa must be lying. 

With that we have 2 lying girls viz. Amanda and Vanessa & Eva as innocent girl telling the truth. Therefore, other innocent girl must be Melinda who must be telling the truth. 

So, as per innocent Melinda, Vanessa isn't a man's sister, hence Amanda must be. And Vanessa is man's girlfriend.

Row Row Row A Tiny RowBoat : Puzzle

Walter, Xavier, Yoshi, and Zeke crossed a river in a tiny rowboat. They all started on the same side of the river. They made three trips from the starting side to the destination side, and two trips from the destination side to the starting side. Here are some facts:

1. On each trip from the starting side of the river to the destination side, two people were in the boat, but only one person rowed the boat, and that person rowed the boat for the entire trip.

2. On each return trip, only one person was in the boat.

3. Walter is the weakest of the group. He could only row the boat if no one else is in it.

4. Xavier is the second weakest of the group. He can only row the boat if he is by himself or if Yoshi, the lightest of the group, is a passenger.

5. Each man rowed the boat at least once. 

Click here for SOLUTION! 

Row Row Row A Tiny RowBoat Puzzle : Solution

What was the puzzle?

We know, Walter, Xavier, Yoshi, and Zeke crossed a river in a tiny rowboat. They all started on the same side of the river. They made three trips from the starting side to the destination side, and two trips from the destination side to the starting side. 

And we have some facts:

1. On each trip from the starting side of the river to the destination side, two people were in the boat, but only one person rowed the boat, and that person rowed the boat for the entire trip.

2. On each return trip, only one person was in the boat.

3. Walter is the weakest of the group. He could only row the boat if no one else is in it.

4. Xavier is the second weakest of the group. He can only row the boat if he is by himself or if Yoshi, the lightest of the group, is a passenger.

5. Each man rowed the boat at least once. 

ANALYSIS :

1] Walter must not had rowed from start to the destination since he is weakest among as per FACT 3. Since, he had to row at least once as per FACT 5, he must had rowed a return tip.


2] The person who had rowed twice, must not had both trips from start to destination. That's because, in that case, he would have had needed third trip in form of return trip to get back to the start once again. So, he must had rowed a return trip at least once.

3] Suppose Walter is the person who rowed the boat twice. Both of his trips must be return trips as concluded in [1] above. 

So if Walter had rowed 2 return trips then each of Xavier, Yoshi and Zeke must have rowed 1 trip from start to the destination. 

If Walter had 'taken' Zeke (while Zeke rowing) across and returned then he would have had to 'take' Yoshi (while Yoshi rowing) across as Xavier being unable to row Walter as per FACT 4. And on returning back to the start after leaving Yoshi across, Walter and Xavier would have had been at the starting point. Now, Walter being unable to row with passenger & Xavier being unable to row Walter, both would have had stuck at the start point.

In short, Walter is not the person for sure who had rowed twice.

4] We know, Walter had one return trip. So the other return trip must have been rowed by someone among Xavier, Yoshi or Zeke. Moreover, the rest of three trips from start to the destination must have rowed by Xavier, Yoshi and Zeke in some order. 

That's how, the one person among Xavier, Yoshi and Zeke, must have rowed twice, one trip from source to destination and other one return trip.

5] If Xavier had rowed twice, then with one trip he must have taken Yoshi across and in other trip he must have returned as we found the fact in [2] above. So, two return trips 'occupied' by Walter and Xavier, Yoshi wouldn't have got a chance to row which is mandatory.

So, Xavier is not the person who had rowed twice.

6] Suppose Zeke is the person who had rowed twice. He must had rowed Walter across the river to give a chance to row his return trip. After Walter reaching at the start, Xavier must had rowed Yoshi across the river thereby completing his compulsory rowing trip.

Then Zeke must have returned to the start to take Walter across then Yoshi would have been the person who hadn't rowed which is against FACT 5.

Therefore, Zeke must not be the person who rowed twice.

7] So, Yoshi must be the person who rowed twice. 

POSSIBILITY 1 : Zeke took Walter across to give him row trip in return. Then, Xavier rowed Yoshi across and Yoshi returned back to take Walter across.

POSSIBILITY 2 : First Xavier rowed Yoshi across and Yoshi returned back after which Zeke takes Walter across to allow Walter to have return trip, and finally, Yoshi taking Walter across the river.

POSSIBILITY 3 : Yoshi took Walter across the river and Walter returned. Zeke rowed Walter across and Yoshi returned to give Xavier a chance to row him across.

The Tunnel Trouble!

A man needs to go through a train tunnel to reach the other side. He starts running through the tunnel in an effort to reach his destination as soon as possible. When he is 1/4th of the way through the tunnel, he hears the train whistle behind him. 

Assuming the tunnel is not big enough for him and the train, he has to get out of the tunnel in order to survive. We know that the following conditions are true - 

1. If he runs back, he will make it out of the tunnel by a whisker.

2. If he continues running forward, he will still make it out through the other end by a whisker.

What is the speed of the train compared to that of the man?

The train must be traveling at THIS speed!

Escape From The Tunnel Trouble!

What was the question?

LOGICAL APPROACH : 

As per condition, if the man runs back he will make it out of the tunnel by a whisker. That means while he runs back 1/4 th tunnel distance, the train travels from it's position to the start of the tunnel. 

In other words, the time taken by man to get back covering 1/4th to the start of the tunnel and the time taken by train to reach at the start of tunnel is same.

So if the man decides to go forward then by time the train reaches at the start of tunnel, man covers another 1/4th tunnel distance i.e. he will be halfway of the tunnel.

At this point of time, the man needs to cover another 1/2th tunnel distance while train has to cover entire tunnel distance. Since, man just manages to escape from accident with train at the exit of tunnel, the train speed has to be double than man's speed as it has to travel distance double of that man travels.

MATHEMATICAL APPROACH : 

Let us suppose - 

M - Speed of Man

T - Speed of Train

D - Tunnel Distance/length

S - Distance between train and the start of tunnel.

As per condition 1, 

Time needed for man to get back at the start of tunnel = Time needed for train to cover distance F to arrive at the start of tunnel

(D/4)/M = S/T  

D/4M =  S/T  .....(1)

As per condition 2,

Time needed for man to move forward at the end of tunnel = Time needed for train to cover distance S + time needed to cover tunnel distance.

(3D/4)/M = S/T + D/T 

Putting S/T = D/4M,

3D/4M - D/4M = D/T

2D/4M = D/T

T/M = 2

T = 2M.

That is speed of the train needs to be double of the speed of the man.

Interestingly, from (1),

D/S = 4M/T

D/S = 2 

D = 2S

S = D/2

That is train is 1/2th tunnel distance away from the start of tunnel. 

Story of Man Having 2 Girlfriends

A man who lives in Middletown has two girlfriends, one in Northtown and one in Southtown. 

Trains from the Middletown train station leave for Northtown once every hour. Separate trains from the station also leave for Southtown once every hour. No trains go to both Northtown and Southtown.

Each day he gets to the Middletown train station at a completely random time and gets onto the first train that is going to either Northtown or Southtown, whichever comes first.

After a few months, he realizes that he spends 80% of his days with his girlfriend from Northtown, and only 20% of his days with his girlfriend from Southtown.

How could this be?

THIS could be the reason behind it! 

Behind Unfair The Number of Visits

What's the story behind the title?

The man arrives at Middletown train station at a completely random time of the day. 

Let's take a look at what happens when he arrives at random time of the day.

After arrival on the station, he is likely to get the train in next hour for sure.

After arriving at random time, there are 80% chances that the first train arriving at the station is heading towards Northtown and 20% chances are there the train is heading towards the Southtown. 

That is there has to be 80% minutes of hour (80% of 60 = 48 minutes) where the first train after is heading towards Northtown and 20% minutes of hour where the next train is heading towards Southtown (20% of 60 = 12 minutes).

So, the trains heading towards the Southtown must be scheduled 12 minutes apart from train heading towards the Northtown.

For example, if trains heading to Northtown are scheduled at 9:00 AM, 10:00 AM, 11:00 AM.......etc then the trains to the Southtown must be scheduled at 9:12 AM, 10:12 AM, 11:12 AM.....etc.

With arrival in 48 minutes past 9:12 AM, 10:12 AM etc, he must be getting the Northtown train and if arrived in 12 minutes past 9:00 AM,10:00 AM etc, he would be getting the Southwest train.

Remember, the timing given are for examples only. The Northwest trains may be scheduled at 9:48 AM, 10:48 AM,......etc and Southwest may be scheduled at 10:00 AM, 11:00 AM.

Key is they leave 12 minutes apart, so that 60 minutes of hour are divided into 48 minutes ahead of Northwest train and 12 minutes ahead of Southwest train. 

Solve The Picure Equation!

Can you find correct number for '?' ?

Here is the solution!

Solution of Picture Equation!

What was the equation?

From picture, it is clear that,

Pair of shoes = 20, single shoe = 10

Man = 5

Goggles = 2

Single Glove = 20

Now, equation in question has man with 2 shoes, 2 gloves and 1 goggles hence his value in equation = 20 + 40 + 5 + 2 = 67

Hence, final equation appears as

10 + 67 x 2 = 144.

 
The answer is 144.

How it Will Affect the Water Level?

A man stuck in a small sailboat on a perfectly calm lake throws a stone overboard. It sinks to the bottom of the lake.

When the water again settles to a perfect calm, is the water level in the lake higher, lower, or in the same place compared to where it was before the stone was cast in?

Did you think it will rise? 

Physics : Finding the Effect on the Water Level

But why water level was affected?

Do you recall what does Archimedes Principle state? For an object to float on water, it has to displace that much volume of water whose weight is equal to weight of the object itself. Now if object has less density than water then obviously it has to displace lesser amount of volume of water to float on it. That means it has to sink less in water.

For a moment, let's assume the stone has very high density & hence having weight equal to hundreds of kilograms despite of having small volume.

Here, stone sinks to the bottom of the lake suggests that it is has more density than water. It can't displace the water whose weight is equal to it's weight.But when it was on sailboat it could push the sailboat down so that more water is displaced weighing equal to it's weight. Result of this, the sailboat sinks little 'deeper' compared to when stone wasn't there.

Obviously, the volume of displaced water when stone was in sailboat (due to stone only) must be greater that the volume of displaced water when stone sinks to the bottom of the lake. That's why both sailboat and stone together could float on the water. In short, sailboat helped stone to displace amount of water needed to float which results in rise in shoreline.

And when stone is thrown out of the sailboat, then ideally it can't displace more water than when it was on sailboat. Now, sailboat sinks less 'deeper' in water displacing only water need to float itself. 

That's why the water level must be dropped compared to earlier. The little rise due to water displaced by stone can't exceed the earlier water level for the reason explained above.

Help The Policeman in Finding The Culprit

Late one evening, a car ran over a pedestrian in a narrow bystreet and drove away without stopping. A policeman who saw the vehicle leave the scene of the accident reported it moving at very high speed. The accident itself was witnessed by six bystanders. They provided the following conflicting accounts of what had happened:

• It was a blue car, driven by a man;
• The car was moving at high speed, its headlights were turned off;
• The car did have license plates, it wasn’t going very fast;
• It was a Toyota, it’s headlights were turned off;
• The car didn’t have license plates, the driver was a woman;
• It was a gray Ford.

When the the car and its driver were finally apprehended, it turned out that only one of the six eyewitnesses gave a fully correct description. Each of the other five provided one true and one false piece of information.

Keeping that in mind, can you determine the following:

— What was the car’s brand?

— What color was the car?

— Was the car going fast or slow?

— Did it have license plates?

— Were its headlights turned on?

— Was the driver a man or a woman? 

Read all the answers here!

To Help The Policeman in Finding The Culprit

But why he needs help? 

Let's recollect all the statements made by all 6 bystanders.

 1.It was a blue car, driven by a man.

 2.The car was moving at high speed, its headlights were turned off.

 3.The car did have license plates, it wasn’t going very fast.

 4.It was a Toyota, it’s headlights were turned off.

 5.The car didn’t have license plates, the driver was a woman.

 6 It was a gray Ford (It was gray car; it was Ford).

-----------------------------------------------------------------------------------

If we believe in report made by Policeman where he stated that the car was moving at very high speed; then the part of the Statement 3 made by third bystander where he says car wasn't going fast turns out to be false. Hence, other part of his statement must be true. So the car must have license plates.

If the car has license plates; then 1st part of the Statement 5 will be false & other part must be true. Hence, the driver must be a woman.

If the driver was a woman, then 2nd part of the Statement 1 turns false making part 1 to be true. Hence, the color of the car must be blue.

If the car was at high speed then the entire Statement 2 must be true or it's 2nd part must be false.

Let's assume 2nd part of the statement 2 be false. Then 2nd part of statement 4 also must be false leaving 1st part to be true. That means the car was Toyota. But this makes statement 6 entirely false (as we already know color of car is blue). This contradicts the crucial data given - Each of the other five provided one true and one false piece of information. In the case, there will be no eyewitness giving full correct description.

So the entire Statement 2 must be true. Hence, the car was with it's headlight off.

If headlights were turned off then 2nd part of the Statement 4 must be true and 1st part false. That means, car wasn't Toyota.

And if car wasn't Toyota, as per Statement 6, it must be Ford but not of gray color.
This matches our early conclusion where we concludes color of the car was blue.

Conclusions:

1.What was the car’s brand?

   - Ford

2.What color was the car?

   - Blue

3.Was the car going fast or slow?

   - Fast

4.Did it have license plates?

   - Yes, it had.

 

5.Were its headlights turned on?

   - No, those were off.

6.Was the driver a man or a woman?

   - A woman. 

A Railway And Cyclist Crossing

A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. 

What was the speed of the train?

Skip To Know The Speed Of The Train! 

To Cross The Cyclist...

What was the scenario?

 Let's suppose he reaches the crossing at 9:00 AM. Usually at 8:30 AM he is at point A, 6 miles before the usual crossing point B (speed of 12 mph, means 6 mile per half hour).

On the day on which he was late by 25 minutes, he must be again at point A (i.e. 6 miles ahead of usual crossing point B) at 8:55 AM. So at this point, both train and man were at the same point A. And the train as everyday, reaches point B at 9:00 AM. That means, it travels 6 miles in 5 minutes. Hence, train must be traveling at 72 mph.  

"Thanks,You're Fired!"

A man is leaving on a business trip and stops by his office on the way to the airport. The night watchman stops him and says, "Sir, don't take that flight. I had a dream last night that your plane would crash and everyone would die!" The business man cancels his trip and sure enough, the plane crashes, killing all the passengers. The man gives his watchman a $10,000 reward for saving his life, then fires him. Why?

That's why! 

Source 

This Is Not Allowed On Duty

What exactly happened? 

The man awarded $10000 obviously for saving his life. The duty of night watchman is to keep watch on office at night not to sleep & dream.

That's why he fires the watchman.