Crack The 10-Digits Password

In an attempt to further protect his secret chicken recipe, Colonel Sanders has locked it away in a safe with a 10-digit password.  Unable to resist his crispy fried chicken, you'd like to crack the code. 

Try your luck using the following information:

All digits from 0 to 9 are used exactly once.

No digit is the same as the position which it occupies in the sequence.

The sum of the 5th and 10th digits is a square number other than 9.

The sum of the 9th and 10th digits is a cube.

The 2nd digit is an even number.

Zero is in the 3rd position.

The sum of the 4th, 6th and 8th digits is a single digit number.

The sum of the 2nd and 5th digits is a triangle number.

Number 8 is 2 spaces away from the number 9 (one in between).

The number 3 is next to the 9 but not the zero.

Click here to know how to CRACK it! 

Cracking The 10-Digits Password

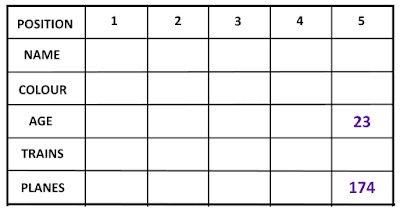
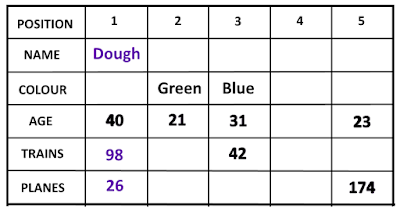
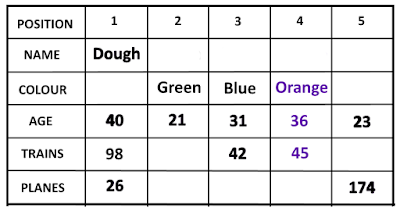
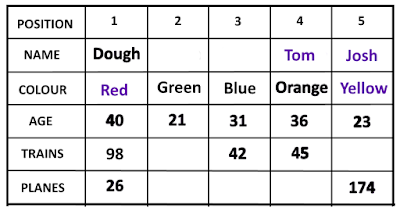
What was the challenge? 

Let's suppose the 10-digits password is ABCDEFGHIJ.

---------------------------------

Take a look at the given clues to crack down the password.

1. All digits from 0 to 9 are used exactly once.

2. No digit is the same as the position which it occupies in the sequence.

3. The sum of the 5th and 10th digits is a square number other than 9.
 
4. The sum of the 9th and 10th digits is a cube.
 
5. The 2nd digit is an even number.
 
6. Zero is in the 3rd position.
 
7. The sum of the 4th, 6th and 8th digits is a single digit number.
 
8. The sum of the 2nd and 5th digits is a triangle number.
 
9. Number 8 is 2 spaces away from the number 9 (one in between).
 
10. The number 3 is next to the 9 but not the zero. 

--------------------------------------

STEPS : 

Respective Clues are in ().

1] Since, every digit is used only once (1), the sum of 2 digits can't exceed 
9 + 8 = 17 and minimum sum of 2 digits can be only 0 + 1 = 1.

2] So, the sum of 5th & 10th digits which is square (3) can be - 1, 4, 16.
The sum of 9th & 10th digits which is cube (4) can be - 1, 8.
The sum of 2nd & 5th digits which is triangle number (8) can be - 1, 3, 6, 10, 15.

3] As per (6), 0 is already at third position i.e. C = 0. Hence, 2nd, 5th, 9th or 10th digits can't be 0. Therefore, the sum of 5th & 10th or 9th & 10th or 2nd & 5th can't be 1. Revising list of possible values of those in step 2.

The sum of 5th & 10th digits which is square (3) can be -  4, 16.
The sum of 9th & 10th digits which is cube (4) can be -  8.
The sum of 2nd & 5th digits which is triangle number (8) can be -  3, 6, 10, 15.

4] Possible pairs of 9th & 10th digits - (1,7), (7,1), (2,6), (6,2), (3,5), (5,3)

If IJ = 71, then 5th digit E must be 4 - 1 = 3 & possible values of 2nd digit B are 0,3,7.
But as per (5), B must be even & C = 0 already.

IJ = 26 or 62 or 35 doesn't leave any valid value for 5th digit E.

If IJ = 53, then 5th digit E must be 1 & possible values of 2nd digit B are 2,5,9
That is B = 2 (5). But as per (2), no digit is the same as the position which it occupies in the sequence. So, the number 2 can't be at 2nd position where B is there.

Hence, IJ must be 17 i.e. I = 1, J = 7.

5] This leaves only 9 as valid value for 5th digit E so that (3) is true. 

So, E = 9 and hence B = 6 with sum of 2nd digit B and 5th digit E as 15.

6] So far, we have, B = 6, C = 0, E = 9, I = 1 and J = 7. 

As per (10), the number 3 is next to the 9 but not the zero. Hence, the 6th digit F must be 3. F = 3.

7] As per (9), the 8 is 2 spaces away from 9 i.e. here 5th digit E=9. With 3rd position already occupied by C = 0, the digit 8 must be at 7th position. 
So, G = 8. 

8] As per (7), D + F + H must be single digit. We have, F = 3 already, 
so possible values of D + H are 0, 1, 2, 3, 4, 5, 6.

D + H can't be 0 (0+0), 1 (1+0), 2(1+1/2+0), 3(1+2/3+0), 4(2+2/3+1/4+0), 5(2+3/4+1/5+0) since digits are repeated with C=0, I=1, F=3 already.

Hence, D + H = 6. 

9] Now, D = 5 and H = 1 is not possible. Also, D/H can't be 0 or 6. Both D and H can't be 3 at the same time. D can't be 4 as D is at 4th position. 

Hence, D = 2, H = 4.

10] With B = 6, C = 0, D = 2, E = 9, F = 3, G = 8, H = 4, I = 1, J = 7, the only digit left for the first position A is 5. So A = 5.

CONCLUSION : 

A = 5, B = 6, C = 0, D = 2, E = 9, F = 3, G = 8, H = 4, I = 1, J = 7.

So, the 10-digits password ABCDEFGHIJ is 5602938417.

 

The Spotting Contest

During a recent plane and train spotting contest, five eager entrants were lined up ready to be tested on their spotting ability. 

They had each spotted a number of planes (26, 86, 123, 174, 250) and a number of trains (5, 42, 45, 98, 105). From the clues below, can you determine what colour shirt each was wearing, their position, their age (21, 23, 31, 36, 40) and the number of trains and planes spotted?

1. Bob spotted 44 less trains than planes. 

2. Tom was 36 years old. 

3. The person on the far right was 8 years younger than Bob, and spotted 174 planes. 

4. Josh was wearing a yellow shirt and spotted 37 trains fewer than Bob. 

5. The person who was wearing a green shirt, was 19 years younger than the person to his left. 

6. Steven spotted 105 trains and 250 planes.

7. The person in the center was 31 years old, was wearing a blue shirt and spotted 42 trains.

8. Doug, who was on the far left, spotted 26 planes, and spotted 72 trains more than planes. 

9. The person who was wearing a red shirt was 4 years older than Tom and was not next to the person wearing a blue shirt. 

10.The person who was next to the 31 year old, but not next to the person who spotted 26 planes, was wearing a orange shirt, and spotted 45 trains. 

Here are final STATS of the contest! 

Final Stats of The Spotting Contest

What was the contest?

Five participants having ages (21, 23, 31, 36, 40) had each spotted a number of planes (26, 86, 123, 174, 250) and a number of trains (5, 42, 45, 98, 105). 

Below are the clues given - 


------------------------------------------

1. Bob spotted 44 less trains than planes. 

2. Tom was 36 years old. 

3. The person on the far right was 8 years younger than Bob, and spotted 174 planes. 

4. Josh was wearing a yellow shirt and spotted 37 trains fewer than Bob. 

5. The person who was wearing a green shirt, was 19 years younger than the person to his left. 

6. Steven spotted 105 trains and 250 planes. 

7. The person in the center was 31 years old, was wearing a blue shirt and spotted 42 trains. 

8. Doug, who was on the far left, spotted 26 planes, and spotted 72 trains more than planes. 

9. The person who was wearing a red shirt was 4 years older than Tom and was not next to the person wearing a blue shirt. 

10. The person who was next to the 31 year old, but not next to the person who spotted 26 planes, was wearing a orange shirt, and spotted 45 trains. 

------------------------------------------

STEPS : 

Let's make at table like below and fill the data one by one.

 
STEP 1 : 

As per (3), the person on the far right that is at position 5 had spotted 174 planes & he must be 23 years old so that Bob aged 31 years (only pair of ages having 8 years difference.

 
STEP 2 : 

As per (7), the person at position 3 who is wearing blue shirt and is 31 year old. He has spotted 42 trains.

STEP 3 : 

For (5) to be true, the ages of those participants occupying consecutive positions must be 40 and 21 respectively. Only, positions lefts for (5) to be true are 1 & 2.

STEP 4 : 

And as per (8), the person at position 1 must be Dough who spotted 26 planes and spotted 72  trains more than planes i.e. 26 + 72 = 98 trains.

STEP 5 : 

As per (10), the person at position 4 must be wearing orange shirt and must have spotted 45 trains. His age must be 36 years (only number in ages list left).

STEP 6 :

As per (9) suggests, Tom must be 36 years old positioned at 4 and Dough must be the person wearing red shirt. With that, Josh in (4) must be wearing yellow shirt and positioned at no.5. 

STEP 7 : 

The hint (4), also suggests that Josh must had spotted 5 trains out of 42-5 possible spotted trains pair shared with Bob. Hence, the person at 2nd position must had spotted 105 trains (only number left in list of number of trains spotted).
 

STEP 8 : 

As per (3), the person having age 31 must be Bob. Hence, at no.2, Steven must be there. 

STEP 9 : 

As per (6), Steven have spotted 250 planes. As per (1), Bob must have spotted 42 + 44 = 86 planes. And the only number left as number of planes spotted for Tom is 123.

STEP 10 :

Final Stats look like as - 

The Race of Multi-Tasking Clowns

Many contestants entered the unicycle race, but only the best multi-tasking clown came out on top, considering that each had to juggle clubs while trying to win the race! Most of the pack were soon disqualified after dropping a club or falling off the unicycle. In the end, four of the best clowns crossed the finish line. 

From this information and the clues below, can you determine each clown's full (real) name, club color (one is silver), and placement?

Places: 1st, 2nd, 3rd, 4th
First Names: Kyle, Matt, Jake, Leon
Surnames: Turner, Pettle, Vertigo, Wheeley
Colors: Green, Orange, Silver, Red

1. Mr. Turner (who isn't Matt) finished one place ahead of the red club juggler.

2. The four are Leon, Mr. Vertigo, the one who juggled with orange clubs, and the one who came in third place.

3. Kyle finished behind (but not one place behind) Mr. Wheeley.

4. Matt and Mr. Pettle finished consecutively, in some order.

5. The one who juggled with green clubs finished two places behind Jake.

Know here final stats of the race! 

In The Race of Multi-Tasking Clowns

What was the puzzle?

Let's take a look at the given data.

------------------------------------------------------------

Places: 1st, 2nd, 3rd, 4th

First Names: Kyle, Matt, Jake, Leon

Surnames: Turner, Pettle, Vertigo, Wheeley

Colors: Green, Orange, Silver, Red


1. Mr. Turner (who isn't Matt) finished one place ahead of the red club juggler.

2. The four are Leon, Mr. Vertigo, the one who juggled with orange clubs, and the one who came in third place.

3. Kyle finished behind (but not one place behind) Mr. Wheeley.

4. Matt and Mr. Pettle finished consecutively, in some order.

5. The one who juggled with green clubs finished two places behind Jake.  

------------------------------------------------------------ 

We will make a table like below and fill it step by step.

 
 STEPS :

1] As per clue (2), Leon, Mr. Vertigo, the one who juggled with orange clubs, and the one who came in third place are supposed to be different. Hence, Leon or Vertigo didn't finish at 3. So, Pettle or Turner must be at 3.

2] But as per (1), Matt isn't a Turner, and as per (4) Matt and Pettle are two different persons. Hence, Matt didn't finish at 3 for sure.

3] As per (3), Mr. Wheely too can't be at 3 as in that case no placement would be left for Kyle. And Jake too can't be at 3 as in that case no placement would be left for the one who juggled with green clubs.

So, if Leon, Matt and Jake aren't at 3 then Kyle must be at 3 having surname Pettle or Turner.

4] With that, Mr. Wheely must have finished first as clue (3) suggests.

5] Now, as per (1), Turner didn't finish at no.4 since there would be no place for red club juggler. Also, as per (4), Pettle can't be at 4 since Matt can't be at 3 (STEP 3). Hence, at no.4, Vertigo is there.

6] As per (2), Vertigo and Leon are 2 different contestants. Also, as per clue (5) Jake can't be at no.4 as in that case there would be no place left for the one who juggled green clubs. Hence, the first name of Vertigo is Matt.

7] Now, clue (4) suggests Pettle is at no.3

8] The only place for the Turner is no.2 and by (1), Kyle Pettle is red club juggler.

9] Now, the only locations left for the contestants pointed by clue (5) i.e. for Jake and green club juggler are 2 and 4.

10] The only location left for Leon is no.1 and as per (2), Leon and orange club juggler are different. Hence, Leon must be a silver club juggler and Jake Turner is orange club juggler.

CONCLUSION : 

So, the final stats of race are - 

   

Cars Around Interesting Circular Track

Around a circular race track are n race cars, each at a different location. At a signal, each car chooses a direction and begins to drive at a constant speed that will take it around the course in 1 hour. When two cars meet, both reverse direction without loss of speed. Show that at some future moment all the cars will be at their original positions.

Here is that proof!


Source 

Analysing Interesting Circular Race Track

What was the interesting fact about?

Just imagine that each car carries a flag on it and on meeting pass on that flag to the next car. Obviously, this flag will move at the constant speed around the track as cars carrying it are also moving at the constant speed. So, the flag will be back at the original position after 1 hour.

Let's assume there are only 2 cars on the track at diagonally opposite points as shown below. 

After 15 minutes, on meeting with Car 2, Car 1 will pass on the flag & both will reverse their own direction. 30 minutes later (i.e. 45 minutes after start) both cars again meet each other and Car 2 will pass on flag back to Car 1 & directions are reversed again. Again in another 15 minutes (i.e. after 1 hour from start), both cars are back at the original positions. 

Now, let's suppose that there are 4 cars on the track positioned as below.

The above image shows how cars will be positioned after different points of time & how they reverse direction after meeting.

Again, all are back to the original position after 1 hour including the flag position. One more thing to note that the orders in which cars are never changes. It remains as 1-2-3-4 clockwise. 

To conclude, for 'n' number of cars, at some point of time all the cars will be in original positions in future.   
 

Owners Of Homes in Home Town

What were the clues? 

To simplify the process, let's number the houses as 1,2,3,4 and separate clues given.

a. Mrs Jennifer's house is somewhere to the left of the green marbles one.
b. The third one along is white marbles.
c. Mrs Sharon owns a red marbles house
d. Mr Cruz does not live at either end.
e. Mr Cruz lives somewhere to the right of the blue marbles house.
f. Mr Danny lives in the fourth house
g. The first house is not made from red marbles.

As per clues (b) and (g), 1 and 3 aren't made of red marbles. Since Danny is living in 4 as per (f), the red house owned by Mrs. Sharon must be positioned at 2.

Since 2 is already occupied, as per (d), Mr. Cruz must be living at number 3 which is of white marbles according to (b).

According to (a), 4 must be green marbles since otherwise Jennifer wouldn't be somewhere at left. As per (f) this 4 th house is owned by Mr.Danny.

The only house left for Jennifer is blue positioned at 1.

To conclude,

Mrs Jennifer - blue marbles at Number 1
Mrs Sharon - red marbles at Number 2
Mr Cruz - white marbles at Number 3
Mr Danny - green marbles at Number 4

Just Try To Crack It!

Can you tell the correct key?

Here is the step-by-step process!

Source 

Cracking of The Code in Steps...

What was the challenge?

Let's number the clues as 1, 2, 3.

Now following step by step process here onward. 

1. The numbers 3 & 1 are common in first & third combinations. Now both must not be the part of original number as in that case Clue 1 will be invalid. 

2. If numbers 3 & 1 are not correct in third combination then the correct 2 numbers must be among 5,7,9.

3. But it can't be both 7 and 9 as again that would make clue 1 invalid! Hence, the 5 is part of the original key & in correct position as in third combination. So we have got first digit of key as a 5.

4. The 1 correct number in clue 2 is 5 & that's in wrong position. If other is assumed to be 9 & to be in right position then it contradict the clue 3. So the second digit must be 7.

5.The only correct number in clue 1 is 7 & that's in wrong position. That means numbers 1,3,4,9 must not be the part of the code.

6. Since 3,4,9 eliminated in previous steps, the only number that is correct and in right position must be 6 in suggestion made by clue 2. So far we have got 3 digits of the code as 576XX.

7. Last 2 digits can be any combination from 0,2,5,7,6,8. Now addition of all digits is equal to the number formed by last 2 digits. It's impossible that the addition of all digits exceeds 50. Hence, the second last digit must be 2.

8. Now both 57620 or 57628 are perfectly valid where sum of all digits equals to number formed by last 2 digits.