Master Plan By Wise Men

Why this master plan needed? 

99 can be guaranteed to save! How?

Even if the person behind calls out the color of the hat that next person is wearing both would be survived only if they are wearing same color of hat. 

So how 99 can be saved?

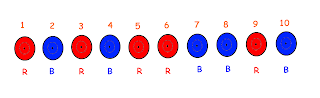
For a simplicity, let's assume there are only 10 wise men & (only) assume we are among them. Now, we need to make a master plan to survive from this game of death.

One of us need to agree to sacrifice his life to save 9 of us & this person would be the first one in line. He will be survived of he has good luck.

The first person in line should shout RED if he founds number of RED hats even otherwise he should shout BLUE. Now if he has good luck then the hat color of his own hat would match & he would be survived.

The clue given by the first person is very important. Right from second person everyone need to count number of RED hats in front of him. Additionally, the next person need to keep track of number of RED hats that people behind him are wearing.
In other words, every person need to think that how the first person counted number of RED hats. Let you be that person. Now the first person count number of RED hats behind you + your hat color (if it's RED) + number of RED hats in front of you.

Now,in our example, the first person counts number of RED hats as 4 & says RED. Luckily his own hat color too is RED & hence he would be survived.Every other one should not count the color of hat that first person is wearing.

Now the second person counts number of RED hats again as 4. Now he should think that if he had RED hat as well then the first person would have counted 5 RED hats. So he need to deduce that his hat must be BLUE.

The king would move to the next person.

The third person need to keep in mind that what second said. Now, here second said BLUE & the number of RED in front of third person is 3 i.e. odd. Hence, he need to deduce that his hat color is RED as only in that case the number of RED hats the first person saw would be even i.e.4. Otherwise, the first person would have counted only 3 RED hats if third person had BLUE hat.

Now the fourth person keeps the track of number of RED he had heard previously (here only once). Now he counts number of RED hats in front of him (here 3) then add it to the number of REDs he had heard (here it is 1). So total number of RED hats according to him is 4 (excluding first person's hat). That is even as first person pointed. Hence he must deduce that he has BLUE hat. If he had RED one then first person would have counted 5 number of RED hats i.e. odd number & would have called out BLUE.

In this way, fifth & sixth need to guess correctly the color of their own hat. 

Let's take look how seventh person would respond as per out plan. He can see only 1 RED hat in front of him. Additionally, he had heard 3 RED s (from 3,4,6). Adding those, according to him number of RED hats (excluding first person's hat) is 3 + 1 = 4. Again, it's even similar to that counted by first person.

In short, if the person has data of number of RED hats (from behind added to that in front) as even (similarly as pointed by first person) then his hat color must be BLUE otherwise RED.

On the similar note, if the first person calls out BLUE & if the person having number of RED hats (adding number of RED hats from behind to that of in front) odd (similarly as pointed by first person) then his hat must be BLUE. And if the person finds that number even then he must be wearing BLUE hat.

One thing to note here is that whatever happened with the previous person doesn't matter here. In fact, every one would be absolutely sure with the survival of every other person except the first person.

What the most important is first person's call & every person's calculations. The later must be very accurate to ensure life of all.  

We can, 'encode' the even or odd nature of number of RED hats or BLUE hats which the first person is going to indicate and accordingly deduce method to correctly determine the color of hat that each person is wearing.

This is how we can ensure 9 survived in 10. With the same plan, 99 can be guaranteed to be survived in 100.