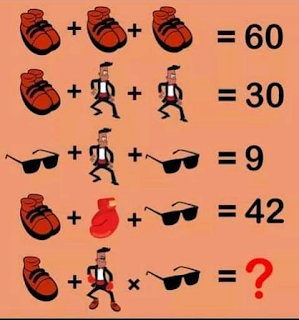मराठी गाणी ओळखा !

मराठी गाणी ओळखा.

      ( एक-दोन गाणी जुनी आहेत
       पण तुम्ही ऐकलेली आहेत)

     उदा. सा वि तु रे म वे हे ला
     उत्तर - सावळ्या विठ्ठला तुझे रे
                 मला वेड हे लागले

👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇

 उत्तरांसाठी येथे टिचकी मारा !

👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆


(1) घ सुं श्री अ झा
(2) गो गो पा फु छा दा म ए व आ
(3) सां क क तु भा मा म
(4) दि म सु न मी सं मा रे
(5) न न आ सु फु
(6) गा वा भि भि पा न न
(7) दा कं ये ओ ये गा
(8) ह ह जो बा पा   पा म झु खे
(9) वा ट इ स्व सं ज थां धा सा घ
(10) सां ये गो सा सा
(11) उ शु चां
(12) रा ही बा ह रा ही बा
(13) म जा द्या घ आ वा की बा
(14) निं झा चं झो गं बा
(15) या ज या ज श प्रे क
     
   गाणी परिचयाची असली तरी
  विचारण्याची पद्धत वेगळी
   असल्याने थोडा वेळ लागेल.



 काहीसा असाच विचार करायला लावणारा  
 👉  मराठी म्हणींचा रंगतदार खेळ !   

नक्की वाचा -
 👉  जावयाची अंगठीची अजब मागणी आणि त्यावर सोनाराने लढवलेली शक्कल !

 👉 वाचा -  गोष्ट विषमासूर नावाच्या राक्षसाची !


👉 हा  MPSC मध्ये विचारला गेलेला प्रश्न  सुटतो का पहा!

आद्याक्षरावरून मराठी गाण्यांची ओळख

काय बरं होता हा खेळ ?

ओळखलीत का सगळी गाणी ?

(1) घ सुं श्री अ झा                      :   घनश्याम सुंदरा श्रीधरा अरुणोदय झाला

(2) गो गो पा फु छा दा म ए व आ  :   गोरी गोरी पान फुलासारखी छान दादा मला एक वहिनी आण

(3) सां क क तु भा मा म              :   सांग कधी कळणार तुला रे भाव माझ्या मनातला

(4) दि म सु न मी सं मा रे            :   दिसते मजला सुखचित्र नवे मी संसार माझा रेखिते

(5) न न आ बा सु फु                   :   नवरी नटली आज बाई सुपारी फुटली

(6) गो गो न मां आ                     :   गोरी गोरी नवरी मांडावा आली

(7) दा कं ये ओ ये गा                  :   दाटून कंठ येतो, ओठांत येई गाणे

(8) ह ह जो बा पा पा म झु खे       :   हलके हलके जोजवा बाळाचा पाळणा, पाळण्याच्या मधोमध फिरतो खेळणा

(9) ह हा नं घ पा त्या दे गो          :   हले हा नंदाघरी पाळणा त्यात देखणा गोजिरवाणा

(10) सां ये गो सा सा                  :   सांज ये गोकुळी सावळी सावळी

(11) उ शु चां                            :    उगवली शुक्राची चांदणी

(12) रा ही बा ह रा ही बा            :   राधा ही बावरी हरीची राधा ही बावरी

(13) म जा द्या घ आ वा की बा  :   मला जाऊ द्या ना घरी आता वाजले की बारा

(14) निं झा चं झो गं                 :   निंबोणीच्या झाडामागे झोपला गं बाई

(15) या ज या ज श प्रे क           :   या जन्मावर या जगण्यावर शतदा प्रेम करावे

काहीसा असाच विचार करायला लावणारा  
 👉  मराठी म्हणींचा रंगतदार खेळ !   

नक्की वाचा -
 👉  जावयाची अंगठीची अजब मागणी आणि त्यावर सोनाराने लढवलेली शक्कल !

 👉 वाचा -  गोष्ट विषमासूर नावाच्या राक्षसाची !


👉 हा  MPSC मध्ये विचारला गेलेला प्रश्न  सुटतो का पहा!

"Spot on the Forehead" Sequel Contest

After losing the "Spot on the Forehead" contest, the two defeated Puzzle Masters complained that the winner had made a slight pause before raising his hand, thus derailing their deductive reasoning train of thought. 

And so the Grand Master vowed to set up a truly fair test to reveal the best logician among them.


He showed the three men 5 hats - two white and three black. 

Then he turned off the lights in the room and put a hat on each Puzzle Master's head. After that the old sage hid the remaining two hats, but before he could turn the lights on, one of the Masters, as chance would have it, the winner of the previous contest, announced the color of his hat. 

And he was right once again.

What color was his hat? What could have been his reasoning? 

The winner is wisest for a reason! 

Master of Logic For a Reason!

How the master was challenged?

Let's assume once again A, B and C are those logicians and C has guessed the color of own hat correctly. Here is what he must have thought - 

============================================================================

"I'm assuming the grand master is conducting this test fairly denying any sort of advantage to any participant.

With that assumption, the grand master can't put 2 white and 1 black hat on heads. In that case, the person having black hat and watching 2 white hats on others' head would know the color of own hat immediately.

For fair play, he can't put 2 blacks and 1 white hat either. That will give unfair advantage to the logicians wearing black hats. Suppose A and B are wearing black and I'm wearing white hat. Now, what A (or B) would be thinking - 

         ---------------------------------------------------------------------------------------------------

       " I'm A (or B) and I can see 1 black and 1 white hat (on head of C). If I have white 
         hat on my head then B (or A) would know color of his hat as black as there are 
         only 2 white hats available and those would be on my head and C's head.

         Moreover, 1 black and 2 white hats already eliminated as it's unfair distribution.

         That means I must be wearing black hat."

         ---------------------------------------------------------------------------------------------------

That's how the combination of 2 black and 1 white hats also eliminated from fair play.

Hence, all of three must be wearing black hats is only fair distribution giving all of us equal chance of winning and hence I must be wearing black hat only. 

============================================================================ 

Note : Here, C is assumed as a winner for only sake of convenience, otherwise either A or B whoever is wisest can be winner.

Spot On The Forehead!

Three Masters of Logic wanted to find out who was the wisest among them. So they turned to their Grand Master, asking to resolve their dispute.

"Easy," the old sage said. "I will blindfold you and paint either red, or blue dot on each man's forehead. When I take your blindfolds off, if you see at least one red dot, raise your hand. The one, who guesses the color of the dot on his forehead first, wins."


And so it was said, and so it was done. 

The Grand Master blindfolded the three contestants and painted red dots on every one. 

When he took their blindfolds off, all three men raised their hands as the rules required, and sat in silence pondering.

Finally, one of them said: "I have a red dot on my forehead."

How did he guess? 

And this is how his logical brain responded! 


Similar kind of puzzles are - 

The Greek Philosophers  

Real Test Of Genius  

Logical Response By Master of Logic!

What was the test?

Let A, B and C be the names of three logicians and C be the logician who correctly guessed the color of dot on forehead. 

Now, this could be the C's logic behind his correct guess - 

"If I had blue dot on my forehead then A and B must had raised hands after looking red dots on the foreheads of other. In case, what A (or B) would have thought? His logic would be -

    "If C is with the blue dot then B (or A) must have raised hand after noticing 
    red dot on my forehead, hence I must have red dot."

So A (or B) would have successfully guessed color of dot on own forehead easily.

But neither A or B not responding that means I must have red dot on my forehead!"  

The logician who guess it correctly could be either A or B not necessarily be C; here it is assumed C is wisest for the sake of convenience.

Solve The Picure Equation!

Can you find correct number for '?' ?

Here is the solution!

Solution of Picture Equation!

What was the equation?

From picture, it is clear that,

Pair of shoes = 20, single shoe = 10

Man = 5

Goggles = 2

Single Glove = 20

Now, equation in question has man with 2 shoes, 2 gloves and 1 goggles hence his value in equation = 20 + 40 + 5 + 2 = 67

Hence, final equation appears as

10 + 67 x 2 = 144.

 
The answer is 144.

Heavier Vs Lighter Balls

We have two white, two red and two blue balls. For each color, one ball is heavy and the other is light. All heavy balls weigh the same. All light balls weigh the same. How many weighing on a beam balance are necessary to identify the three heavy balls? 

You need only 2 weighings! Click here to know how!

Identifying The Heavier/Lighter Balls

What was the task given?

Actually, we need only 2 weighing. 

Weigh 1 red & 1 white ball against 1 blue & 1 white ball. Weighing result between these balls helps us to deduce the relative weights of other balls.
  ----------------------------------------------------------------------------------------------------

Case 1 : 

If this weighing is equal then the weight of red ball and blue ball are different.
That's because the weighing is equal only when there is combination of 
H (Heavy) + L (Light) against L (Light) + H (Heavy). 

Since, one white ball must be heavier than the other white ball placed in other pan, the red & blue balls place along with them must be of 'opposite' weights with respect to the white balls place along with them.

So weigh this red against blue will give us the heavier red (or blue) leaving other red (or blue) as lighter. 

If red (or blue) weighs more in this weighing then the white ball placed with this red (or blue) in first weighing must be lighter than the other white ball placed with blue (or red) ball.  

----------------------------------------------------------------------------------------------------

Case 2 : Red + White > Blue + White.

The white ball in Red + White must be heavier than the white ball in Blue + White.

The reason is if this white was lighter then even heavier red in the Red + White can't weigh more than Blue + White having heavier white. That is H + L can't beat H + H or obviously would equal with H + L!

So we have got the heavier and lighter white balls for sure.

Now, weigh red from Red + White and blue from Blue + White against other red and blue balls left.

     Case 2.1/2.2 : Red + Blue > or < Red + Blue 

     Obviously, red and blue balls in left pan are heavier (or lighter) than those in other.
    
     ------------------------------------------------------------------------------------

     Case 2.3 :  Red + Blue = Red + Blue 

     Obviously, that's because of H + L = L + H.

      But the red is taken from Red + White which was heavier than the Blue + White. 
      Since, L + H (white is heavier as concluded) can't weigh more than H + L
      (other white is lighter as concluded) or L + L, the red in Red + White 
      must be heavier making H + H combination in that pan in first weighing (case 2). 

      So, we got heavier red and lighter blue obviously leaving lighter red 
      and heavier blue in other pan. 

----------------------------------------------------------------------------------------------------

Case 3 : Red + White < Blue + White.

Just replace Red with blue & vice versa in the deduction made in case 2. 

----------------------------------------------------------------------------------------------------

Larger, Smaller or Similar?

Which of the yellow areas is larger?

Here is comparison of areas! 

Both Sharing Equal Area!

Which areas are into comparison?

Actually, areas of both are equal. The diagonal divide the rectangle into 2 halves. So triangle A and A' or B and B' have equal areas.

When diagonal divides the area of main rectangle into 2 halves, area of triangles A (or A') and area of triangle B (or B') are further subtracted from each half to get the areas of the shaded region.

Since equal areas are subtracted from triangles formed by diagonal to get the shaded area, the area of shaded parts are equal. 

 That is from each half area subtracted = A + B = A' + B'.

The Numbered Hats Test!

One teacher decided to test three of his students, Frank, Gary and Henry. The teacher took three hats, wrote on each hat an integer number greater than 0, and put the hats on the heads of the students. Each student could see the numbers written on the hats of the other two students but not the number written on his own hat.

The teacher said that one of the numbers is sum of the other two and started asking the students:

— Frank, do you know the number on your hat?

— No, I don’t.

— Gary, do you know the number on your hat?

— No, I don’t.

— Henry, do you know the number on your hat?

— No, I don’t.

Then the teacher started another round of questioning:

— Frank, do you know the number on your hat?

— No, I don’t.

— Gary, do you know the number on your hat?

— No, I don’t.

— Henry, do you know the number on your hat?

— Yes, it is 144.

What were the numbers which the teacher wrote on the hats?

Here are the other numbers!

Source 

Cracking Down The Numbered Hats Test

What was the test?

Even before the teacher starts asking, the student must have realized 2 facts.

1. In order to identify numbers in this case, the numbers on the hats has to be in proportion i.e. multiples of other(s). Like if one has x then other must have 2x,3x etc.

2. Two hats can't have the same number say x as in that case third student can easily guess the own number as 2x since x-x = 0 is not allowed.

--------------------------------------------------------------------------------------------------

Now, if numbers on the hats were distributed as x, 2x, 3x then the student wearing hat of number 3x would have quickly responded with correct guess. That's because he can see 2 number as x and 2x on others hats and he can conclude his number as x + 2x = 3x since 
2x - x = x is invalid combination (x, x, 2x) where 2 numbers are equal.

Other way, he can think that the student with hat 2x would have guessed own number correctly if I had x on my own hat. Hence, he may conclude that the number on his hat must be 3x.

But in the case, all responded negatively in the first round of questioning. So x, 2x, 3x combination is eliminated after first round.

-------------------------------------------------------------------------------------------------- 

That means it could be x, 3x, 4x combination of numbers on the hats.

In second round of questioning, Henry guessed his number correctly.

If he had seen 3x and 4x on other 2 hats then he wouldn't have been sure with his number whether it is x or 7x.

Similarly, he must not have seen x and 4x as in that case as well he couldn't have concluded whether his number is either 5x or 3x.

But when he sees x and 3x on other hats he can tell that his number must be 4x as 2x (x,2x,3x combination) is eliminated in previous round!

So Henry can conclude that his number must be 4x.

Since, he said his number is 144,

4x = 144

x = 36

3x = 108.

Hence, the numbers are 36, 108, 144.

Divide The Cake Into Equal Parts!

I have just baked a rectangular cake when my wife comes home and barbarically cuts out a piece for herself. The piece she cuts is rectangular, but it’s not in any convenient proportion to the rest of the cake, and its sides aren’t even parallel to the cake’s sides. 

 
I want to divide the remaining cake into two equal-sized halves with a single straight cut. How can I do it?



This is how it can be cut! 

Cutting The Cake Into Equal Parts!

What was the problem? 

Generally, a line drawn through the center of rectangle divides it into 2 equal parts.
Hence, a line drawn through the centers of both rectangles would divide each of them into 2 equal parts as shown below. (To get the center of each rectangle, all we need to do is draw diagonals of both).

Different Kind of Dice Game!

Timothy and Urban are playing a game with two six-sided dices. The dice are unusual: Rather than bearing a number, each face is painted either red  or blue.

The two take turns throwing the dice. Timothy wins if the two top faces are the same color, and Urban wins if they’re different. Their chances of winning are equal.

The first die has 5 red faces and 1 blue face. What are the colors on the second die?

The second die must have 'these' colors!

Die Needed For Different Kind of Dice Game!

What was the different in dice game?

Throwing two six-sided dice produces 36 possible outcomes. Since both Timothy and Urban have equal chances of winning, there are 18 outcomes where top faces are of same color.

Let's assume there are 'x' red faces and (6-x) blue faces on the other dice.

Remember, the first die has 5 red faces and 1 blue face. Then there are 5x ways by which top faces are red & 1(6-x) ways by which they both are blue. But as deduced above, there are 18 such outcomes in total where faces of dice matches color.

Therefore,

5x + 1(6-x) = 18

4x = 12

x = 3

Hence, other die have 3 red colored & 3 blue colored faces.